题目内容
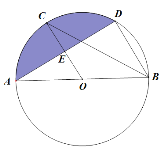
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于( )
A.![]() B.
B.![]() C.4D.3
C.4D.3
【答案】C
【解析】
作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等,得到∠DAE=∠BAF,再证明△ADE≡△ABF,得到DE=BF=10,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=![]() BF=3
BF=3
作AH⊥BC于H,作直径CF,连结BF
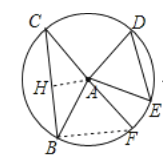
如图, ∵∠BAC+∠EAD=180°,而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF
∴弧DE= 弧BF
∴DE= BF= 6
∴AH⊥BC,
∵CH= BH而CA=AF
∴AH为△CBF的中位线,
∴AH=![]() BF= 3.
BF= 3.
故选:D.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目