题目内容
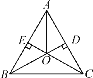
【题目】如图,已知△ABC中,AB=AC=![]() cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
【答案】1或2或(6![]() ﹣9).
﹣9).
【解析】
分三种情况:①∠AQP=90°,②∠APQ=90°,③∠PAQ=90°进行计算即可.
∵AB=AC=![]() cm,∠BAC=120°,
cm,∠BAC=120°,
∴∠B=∠C=30°,BC=![]() =3,
=3,
有三种情况:
①当∠AQP=90°时,
有![]() 或
或![]() ,
,
即![]() 或
或![]()
解得![]()
![]() 或
或![]()
![]() ,
,
②当∠APQ=90°时,这种情况不成立;
③当∠PAQ=90°时,
有![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.
综上所述,当运动时间(单位:秒)为1或2或![]() 或
或![]() 时,△PAQ为直角三角形.
时,△PAQ为直角三角形.
故答案为:1或2或![]() 或
或![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.