Question

（2013•襄城区模拟）如图，△ABC是边长为5的等边三角形，将△ABC绕点C顺时针旋转120°，得到△EDC，连接BD，交AC于F．
（1）猜想AC与BD的位置关系，并证明你的结论；
（2）求线段BD的长．

Answer 1

分析：（1）AC与BD互相垂直平分．如图，连接AD构建菱形ABCD，则菱形的对角线互相垂直平分；
（2）在Rt△BDE中利用勾股定理即可得出BD的长．

解答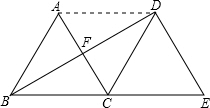：解：（1）AC与BD互相垂直平分．
证明：连接AD，由题意知，△ABC≌△EDC，∠ACE=120°，
又∵△ABC是等边三角形，
∴AB=DC=BC=DE=5，∠ABC=∠ACB=∠DCE=∠E=60°，
∴∠ACE+∠ACB=120°+60°=180°，
∴B、C、E三点在一条直线上．
∴AB∥DC，
∴四边形ABCD为菱形，
∴AC与BD互相垂直平分；

（2）由（1）知，四边形ABCD为菱形，
∴∠DBE=

1

2

∠ABC=30°，
∵∠DBE+∠BDE+∠E=180°，
∴∠BDE=90°．
∵B、C、E三点在一条直线上，
∴BE=10，
∴BD=

BE2-DE2

=

102-52

=5

3

．

点评：本题考查的是等边三角形的性质及旋转的性质，熟知图形旋转后的图形与原图形全等的性质是解答此题的关键．