题目内容
【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE![]() BC(已知),
BC(已知),
∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF![]() ( ).
( ).
∴∠B+∠BFE=180°( ).
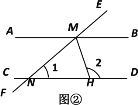
(2)如图②,AB![]() CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.

【答案】(1)见解析;(2)![]()
【解析】
(1)根据两直线平行,同位角相等可推出∠1=∠B,从而得出∠1=∠2,根据内错角相等,两直线平行推出EF∥AB,再根据两直线平行,同旁内角互补即可得出结论;
(2)根据两直线平行,同旁内角互补即可求出![]() ,再根据角平分线的定义求出
,再根据角平分线的定义求出![]() ,再根据两直线平行,同旁内角互补即可求出∠2.
,再根据两直线平行,同旁内角互补即可求出∠2.
证明:∵DE∥BC(已知),
∴∠1=∠ B ( 两直线平行同位角相等).
又∵∠2=∠B( 已知 ),∴∠ 1 =∠ 2 .
∴ EF∥ AB ( 内错角相等两直线平行).
∴∠B+∠BFE=180°( 两直线平行同旁内角互补).
(2)∵AB//CD,∠1=40° ,
∴![]() ,即
,即![]() ,
,
∵MH平分∠BMN,
∴![]() ,
,
∵AB//CD ,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目