��Ŀ����
��ͼ��ֱ��OA�뷴����������ͼ���ڵ�A��3��3��������ƽ��ֱ��OA���뷴����������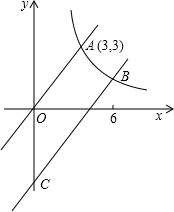 ͼ���ڵ�B��6��m����y�ύ�ڵ�C��
ͼ���ڵ�B��6��m����y�ύ�ڵ�C����1����ֱ��BC�Ľ���ʽ��
��2����A��B��C����Ķ��κ����Ľ���ʽ��
��3���辭��A��B��C����Ķ��κ���ͼ��Ķ���ΪD���Գ�����x��Ľ���ΪE��
�ʣ��ڶ��κ����ĶԳ������Ƿ����һ��P��ʹ��O��E��PΪ��������������BCD���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��������1�����ݵ�A�����꣬����ȷ��ֱ��OA�Լ������������Ľ���ʽ���������÷�������������ʽ����ȷ����B�����꣬��OA��BCƽ�У���ô���ǵ�б����ͬ���ɴ˿�ȷ��ֱ��BC�Ľ���ʽ��
��2������ֱ��BC�Ľ���ʽ�����C�����꣬Ȼ������ô���ϵ������ø������ߵĽ���ʽ��
��3�����ݣ�2�����������ߵĽ���ʽ������ö���D�����꣬���ɵõ�BD��BC��CD�ij������ù��ɶ����涨�������ж���BCD��ֱ�������Σ��ҡ�BDC=90�㣬���������߶Գ��᷽�̿ɵõ�E�����꣬���������OE�ij�������O��E��PΪ��������������BCD���ƣ���֪��BDC=��PEO=90�㣬��ô�����������Ҫ���ǣ�
�١�PEO�ס�BDC���ڡ�OEP�ס�BDC��
�����������鲻ͬ���������������ò�ͬ�ı����߶Σ����ɵõ�PE�ij����������P������꣮����Ҫע�����P�������E���Ϸ�Ҳ������E���·���
��2������ֱ��BC�Ľ���ʽ�����C�����꣬Ȼ������ô���ϵ������ø������ߵĽ���ʽ��
��3�����ݣ�2�����������ߵĽ���ʽ������ö���D�����꣬���ɵõ�BD��BC��CD�ij������ù��ɶ����涨�������ж���BCD��ֱ�������Σ��ҡ�BDC=90�㣬���������߶Գ��᷽�̿ɵõ�E�����꣬���������OE�ij�������O��E��PΪ��������������BCD���ƣ���֪��BDC=��PEO=90�㣬��ô�����������Ҫ���ǣ�
�١�PEO�ס�BDC���ڡ�OEP�ס�BDC��
�����������鲻ͬ���������������ò�ͬ�ı����߶Σ����ɵõ�PE�ij����������P������꣮����Ҫע�����P�������E���Ϸ�Ҳ������E���·���
����⣺��1����ֱ��OA�뷴����������ͼ���ڵ�A��3��3����
��ֱ��OAΪ��y=x��˫����Ϊ��y=
��
��B��6��m������y=
��m=
����B��6��
������1�֣�
��ֱ��BC�Ľ���ʽΪy=x+b����ֱ��BC������B��
��x=6��y=
������y=x+b�ã�b=-
����1�֣�
���ԣ�ֱ��BC�Ľ���ʽΪy=x-
����1�֣�
��2����ֱ��y=x-
�õ�C��0��-
����
�辭��A��B��C����Ķ��κ����Ľ���ʽΪy=ax2+bx-
��A��B������������y=ax2+bx-
���ã�
����1�֣�
���
��1�֣�
���ԣ������ߵĽ���ʽΪy=-
x2+4x-
����1�֣�
��3�����ڣ�
��y=-
x2+4x-
�䷽��y=-
(x-4)2+
��
���Եõ�D��4��
�����Գ���Ϊֱ��x=4��1�֣�
�öԳ�����x�ύ�������ΪE��4��0������1�֣�
��BD=
��BC=
��CD=
����CD2=BC2+BD2�����ԣ���DBC=90�㣨1�֣�
�֡�PEO=90�㣬����O��E��PΪ��������������BCD���ƣ����У�
��
=
����
=
����PE=
����P1��4��
����P2��4��-
��
��
=
����
=
����PE=12����P3��4��12����P4��4��-12����3�֣�
���ԣ���P������Ϊ��4��
������4��-
������4��12������4��-12����
��ֱ��OAΪ��y=x��˫����Ϊ��y=
| 9 |
| x |
��B��6��m������y=
| 9 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
��ֱ��BC�Ľ���ʽΪy=x+b����ֱ��BC������B��
��x=6��y=
| 3 |
| 2 |
| 9 |
| 2 |
���ԣ�ֱ��BC�Ľ���ʽΪy=x-
| 9 |
| 2 |
��2����ֱ��y=x-
| 9 |
| 2 |
| 9 |
| 2 |
�辭��A��B��C����Ķ��κ����Ľ���ʽΪy=ax2+bx-
| 9 |
| 2 |
��A��B������������y=ax2+bx-
| 9 |
| 2 |
|
���
|
���ԣ������ߵĽ���ʽΪy=-
| 1 |
| 2 |
| 9 |
| 2 |
��3�����ڣ�
��y=-
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
���Եõ�D��4��
| 7 |
| 2 |
�öԳ�����x�ύ�������ΪE��4��0������1�֣�
��BD=
| 8 |
| 72 |
| 80 |
�֡�PEO=90�㣬����O��E��PΪ��������������BCD���ƣ����У�
��
| OE |
| BC |
| PE |
| DB |
| 4 | ||
6
|
| PE | ||
2
|
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
��
| OE |
| DB |
| PE |
| BC |
| 4 | ||
2
|
| PE | ||
6
|
���ԣ���P������Ϊ��4��
| 4 |
| 3 |
| 4 |
| 3 |
���������⿼�����ô���ϵ����ȷ����������ʽ�ķ���������ͼ���ϵ���������塢ֱ�������ε��ж������������ε��ж������ʵ�֪ʶ��Ҫע����ǣ�3�����У������������εĶ�Ӧ�ߺͶ�Ӧ�Dz�ȷ�����������Ҫ�������ۣ�����©�⣮

��ϰ��ϵ�д�
 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
�����Ŀ
 ��ͼ��ֱ��OA�뷴��������y=
��ͼ��ֱ��OA�뷴��������y= ��ͼ��ֱ��OA�뷴��������y=
��ͼ��ֱ��OA�뷴��������y= ͼ���ڵ�B��6��m����y�ύ�ڵ�C��
ͼ���ڵ�B��6��m����y�ύ�ڵ�C��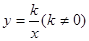 ��ͼ���ڵ�һ������A�㣬AB��x���ڵ�B����OAB�����Ϊ2����k��
��ͼ���ڵ�һ������A�㣬AB��x���ڵ�B����OAB�����Ϊ2����k��