题目内容
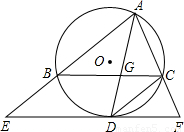
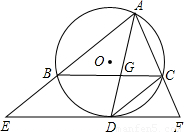
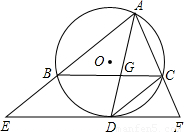
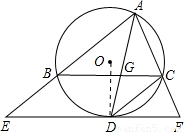
（2004•淮安）已知：如图，在△ABC中，∠BAC的平分线AD交△ABC的外接圆⊙O于点D，交BC于点G．（1）连接CD，若AG=4，DG=2，求CD的长；
（2）过点D作EF∥BC，分别交AB、AC的延长线于点E、F．求证：EF与⊙O相切．
【答案】分析：（1）可通过证△CGD∽△ACD，得出AG、GD、CD的对应比例关系，即可求出CD的长；
（2）连接OD，证OD⊥EF即可．
解答：（1）解：∵AD平分∠BAC
∴∠DAB=∠DAC
∵∠DAB和∠DCB对同弧
∴∠DAB=∠DCB，
即∠DCG=∠DAB
∴△ACD∽△CGD，
∴
∴CD2=DG•DA=2•（2+4）=12
∴CD=2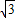
；
（2）证明：连接OD，
∵∠DAC=∠DAB
∴D为弧BC的中点
∴OD⊥BC
∵BC∥EF
∴OD⊥EF
∴EF与⊙O相切．
点评：本题主要考查了圆周角定理、切线的判定、垂径定理、相似三角形的判定和性质等知识点．
（2）连接OD，证OD⊥EF即可．
解答：（1）解：∵AD平分∠BAC
∴∠DAB=∠DAC
∵∠DAB和∠DCB对同弧
∴∠DAB=∠DCB，
即∠DCG=∠DAB
∴△ACD∽△CGD，
∴
∴CD2=DG•DA=2•（2+4）=12
∴CD=2
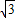；（2）证明：连接OD，
∵∠DAC=∠DAB∴D为弧BC的中点
∴OD⊥BC
∵BC∥EF
∴OD⊥EF
∴EF与⊙O相切．
点评：本题主要考查了圆周角定理、切线的判定、垂径定理、相似三角形的判定和性质等知识点．
练习册系列答案
黄冈创优卷系列答案
相关题目
，求m的值，并求出该函数图象的顶点坐标．
，求m的值，并求出该函数图象的顶点坐标．
