题目内容
 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10).函数y=
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10).函数y=| k | x |
①⊙P与x轴相离; ②△PMN的面积为14;
③⊙P的坐标为(-4,-7); ④k的值为28.
分析:①由M、N两点坐标及⊙P的半径5,根据勾股定理求P点坐标,用P点的纵坐标的绝对值与半径比较即可;②根据MN=ON-OM求△PMN的底边,由MR=
MN,及半径PM=5,运用勾股定理求PR,可求△PMN的面积;③由②中所求线段可求P点坐标;④利用P点坐标求k的值.
| 1 |
| 2 |
解答: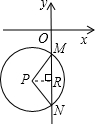 解:由图可知①正确;
解:由图可知①正确;
∵MN=|-10+4|=6,过点P作PR⊥MN,则MR=
MN=3,
∴PR=
=4,∴S△PMN=
×6×4=12,②错;
由OR=OM+MR=7,∴点P坐标为(-4,-7),③正确;
由函数y=
过点P(-4,-7),知k=(-4)×(-7)=28.④正确.
故答案为:①③④.
 解:由图可知①正确;
解:由图可知①正确;∵MN=|-10+4|=6,过点P作PR⊥MN,则MR=
| 1 |
| 2 |
∴PR=
| PM2-MR2 |
| 1 |
| 2 |
由OR=OM+MR=7,∴点P坐标为(-4,-7),③正确;
由函数y=
| k |
| x |
故答案为:①③④.
点评:本题考查圆与反比例函数的综合解题思路.关键是根据垂径定理、勾股定理求P点坐标.

练习册系列答案
相关题目
 如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,
如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,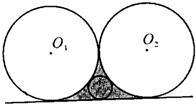 12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于
12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°. 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为