题目内容

甲、乙、丙三位同学用质地大小完全一样的纸片分别制作一张卡片a、b、c，收集后放在一个不透明的箱子中，然后每人从箱子中随机抽取一张．
（1）用列表或画树状图的方法表示三位同学抽到卡片的所有可能的结果；
（2）求三位同学中至少有一人抽到自己制作卡片的概率．
（1）列表或画树状图表示三位同学抽到卡片的所有可能结果如下图；（2）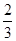
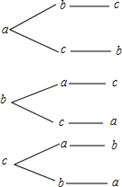
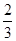
甲
a
a
b
b
c
c
乙
b
c
a
c
a
b
丙
c
b
c
a
b
a

试题分析：先列表或画树状图表示三位同学抽到卡片的所有可能结果，再根据概率公式求解即可.
（1）列表或画树状图表示三位同学抽到卡片的所有可能结果如下：
甲
a
a
b
b
c
c
乙
b
c
a
c
a
b
丙
c
b
c
a
b
a

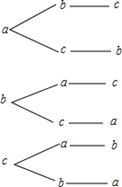
（2）如图可知，三位同学抽到卡片的所有可能的结果共有6种，
所以三位同学中有一人抽到自己制作的卡片有3种，有三人都抽到自己制作的卡片有1种．
所以三位同学中至少有一人抽到自己制作卡片有4种．
所以三位同学中至少有一人抽到自己制作的卡片的概率为．
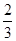点评：解题的关键是熟练掌握概率的求法：概率=所求情况数与总情况数的比值.
练习册系列答案
相关题目
一只蝴蝶在空中飞行，然后随意落在如图所示的某一方格中（每个方格除颜色外完全相同），则蝴蝶停止在白色方格中的概率是      .
如图，在一块△ABC板面中，将△BEF涂黑，其中点D、E、F分别为BC、AD、CE的中点，小华随意向△ABC板面内部射击一粒小弹丸，则弹丸击中黑色区域的概率是　　　　．
屏幕上有四张卡片，卡片上分别有大写的英文字母“A，Z，E，X”，现已将字母隐藏只要用手指触摸其中一张，上面的字母就会显现出来  某同学任意触摸其中2张，上面显现的英文字母都是中心对称图形的概率是________  
某商场为了“五一”促销，举办抽奖活动，抽奖方案是：将如图的正六边形转盘等分成6个全等三角形，其中两个涂上灰色，顾客任意转动这个转盘2次，当转盘停止时，两次都指向灰色区域的即可获得奖品．

（1）求顾客获得奖品的概率；
（2）商场工作人员又提出了以下几个方案：
①抛掷一枚均匀的硬币3次，3次抛掷的结果都是正面朝上的即可获得奖品；
②一只不透明的袋子中，装有10个白球和20个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色后放回袋中并搅匀，再从中摸出一个球，两次都摸出白球的即可获得奖品；
③一只不透明的袋子中，装有2个白球和4个红球，这些球除颜色外都相同，搅匀后从中任意摸出两个球，两个都是白球的即可获得奖品；
④任意抛掷一枚均匀的骰子两次，两次朝上的点数都是3的倍数的即可获得奖品；
这几种方案中和原方案获奖概率相同的有    （填序号）．
将背面完全相同，正面上分别写有数字1、2、3的三张卡片混合后，小明从中随机地抽取一张，把卡片上的数字作为被减数，将形状、大小完全相同，分别标有数字1、2的两个小球混合后，小华从中随机地抽取一个，把小球上的数字作为减数，然后计算出这两个数的差．
(1)请你用画树状图或列表的方法，求这两数差为0的概率；
(2)小明与小华做游戏,规则是:若这两数的差为正数,则小明赢；否则,小华赢.你认为该游戏公平吗?请说明理由.
在无锡市首届“文明风尚好少年”全媒体选拔大赛初赛中，甲、乙、丙三位评委对小选手的综合表现，分别给出“待定”（用字母W表示）或“通过”（用字母P表示）的结论．
（1）请用树状图表示出三位评委给小选手乐乐的所有可能的结论；
（2）对于小选手乐乐，只有甲、乙两位评委给出相同结论的概率是多少？
（3）比赛规定，三位评委中至少有两位给出“通过”的结论，则小选手可入围进入复赛，问乐乐进入复赛的概率是多少？
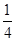一个不透明的口袋中，装有红球6个，白球9个，黑球3个，这些球除颜色不同外没有任何区别．现从中任意摸出一个球，要使摸到黑球的概率为，需要往这个口袋再放入同种黑球        个．
甲.乙二人参加某体育项目训练，为了便于研究，把最近五次训练成绩绘制成如图所示的折线图，下面的结论错误的是（     ）
A．乙的第二次成绩与第五次成绩相同
B．第三次测试甲的成绩与乙的成绩相同
C．第四次测试甲的成绩比乙的成绩多2分
D．由表可以看出，甲的成绩稳定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网