题目内容
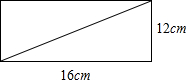
 用纸板剪一个长为16cm,宽为12cm的长方形,再沿对角线把它分成两个三角形(如图),用这两个三角形拼成各种三角形和四边形并计算它们的周长,则最大的周长是
用纸板剪一个长为16cm,宽为12cm的长方形,再沿对角线把它分成两个三角形(如图),用这两个三角形拼成各种三角形和四边形并计算它们的周长,则最大的周长是
- A.64cm
- B.56cm
- C.72cm
- D.84cm
C
分析:根据勾股定理求出对角线的长为 =20(cm),则得两个全等三角形,其边长为12cm、16cm、20cm,从各边长可以得到周长最长的三角形或四边形的周长为(16+20)×2=72(cm),
=20(cm),则得两个全等三角形,其边长为12cm、16cm、20cm,从各边长可以得到周长最长的三角形或四边形的周长为(16+20)×2=72(cm),
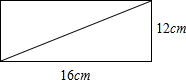
解答:如图所示:已知一个长为16cm、宽为12cm的长方形,
∴根据勾股定理得:对角线的长为 =20(cm),
=20(cm),
那么拼出各种三角形和四边形的周长有以下情况:
(12+16)×2=56(cm),
(12+20)×2=64(cm),
(16+20)×2=72(cm),
所以周长最大的是72cm,
故选:C.
点评:此题考查的知识点是勾股定理,解答此题的关键是先根据勾股定理求出对角线的长,再计算出拼出的三角形和四边形的周长得出正确选项.
分析:根据勾股定理求出对角线的长为
 =20(cm),则得两个全等三角形,其边长为12cm、16cm、20cm,从各边长可以得到周长最长的三角形或四边形的周长为(16+20)×2=72(cm),
=20(cm),则得两个全等三角形,其边长为12cm、16cm、20cm,从各边长可以得到周长最长的三角形或四边形的周长为(16+20)×2=72(cm),解答:如图所示:已知一个长为16cm、宽为12cm的长方形,
∴根据勾股定理得:对角线的长为
 =20(cm),
=20(cm),那么拼出各种三角形和四边形的周长有以下情况:
(12+16)×2=56(cm),
(12+20)×2=64(cm),
(16+20)×2=72(cm),
所以周长最大的是72cm,
故选:C.
点评:此题考查的知识点是勾股定理,解答此题的关键是先根据勾股定理求出对角线的长,再计算出拼出的三角形和四边形的周长得出正确选项.

练习册系列答案
相关题目
 用纸板剪一个长为16cm,宽为12cm的长方形,再沿对角线把它分成两个三角形(如图),用这两个三角形拼成各种三角形和四边形并计算它们的周长,则最大的周长是( )
用纸板剪一个长为16cm,宽为12cm的长方形,再沿对角线把它分成两个三角形(如图),用这两个三角形拼成各种三角形和四边形并计算它们的周长,则最大的周长是( )