题目内容
【题目】如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．
结论：BF= ．
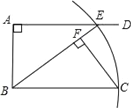
【答案】BF=AE，证△ABE≌△FCB
【解析】试题分析：由题意可得BE=BC，∠AEB=∠FBC，易证明得直角三角形ABE与直角三角形FCB全等，即可得BE=AE．
试题解析：结论：BF=AE．
证明：∵CF⊥BE，
∴∠BFC=90°，
又∵AD∥BC，
∴∠AEB=∠FBC；
由于以点B为圆心，BC长为半径画弧，
∴BE=BC，
在△ABE与△FCB中，
∴△ABE≌△FCB（AAS），
∴BF=AE．
结论：BF=AE．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
【题目】小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题：
（1）小丽买了自动铅笔、记号笔各几支？
（2）若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案？
商品名 | 单价（元） | 数量（个） | 金额（元） |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
