题目内容
阅读下列材料.对于一元二次方程ax2+bx+c=0(a≠0),当△=b2-4ac>0时,记方程两根分别为x1,x2,则有:
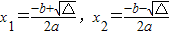 .发现:
.发现: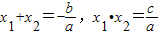 ,
,如图:若一元二次方程
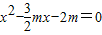 的两实数根分别是A点,B点的坐标,即x1,x2,且x1<0<x2,(AO+OB)2=12•OC+1.
的两实数根分别是A点,B点的坐标,即x1,x2,且x1<0<x2,(AO+OB)2=12•OC+1.(1)求m的值并求出x1,x2.
(2)在前面的条件下,若过O作数轴的垂线,D为垂线上一点,取OD=OC,连AD,BD,试说明AD与BD的位置关系,这样的D点有几个,画图说明.

【答案】分析:(1)利用根与系数的关系得出(x1+x2)2-4x1x2=25,进而得出m的值,进而求出方程的根;
(2)利用数形结合以及勾股定理求出AD与BD的位置关系即可.
解答:解:(1)∵(AO+OB)2=12•OC+1,
∴(-x1+x2)2=12×2+1,
∴(x1+x2)2-4x1x2=25,
∵x1+x2= m,
m,
x1x2=-2m,
∴( m)2+8m=25,
m)2+8m=25,
整理得出:
9m 2+32m-100=0,
(9m+50)(m-2)=0,
解得:m1=- ,m2=2,
,m2=2,
当m1=- 时,△<0,故舍去,
时,△<0,故舍去,
当m2=2时,△>0,
∴方程为:x2-3x-4=0,
解得:x1=-1,x2=4;
(2)∵如图所示,x1=-1,x2=4,CO=2,
∴AO=1,OB=4,DO=CO=2,
∵AD2=AO2+DO2=1+4=5,BD2=DO2+BO2=4+16=20,
AB 2=25,
∴AD2+BD2=AB 2,
∴AD⊥BD,
如图所示这样的D点有2个.
点评:此题主要考查了根与系数的关系以及勾股定理和十字相乘法解一元二次方程,将根与系数的关系与代数式相结合解题是一种经常使用的解题方法.
(2)利用数形结合以及勾股定理求出AD与BD的位置关系即可.
解答:解:(1)∵(AO+OB)2=12•OC+1,
∴(-x1+x2)2=12×2+1,
∴(x1+x2)2-4x1x2=25,
∵x1+x2=
 m,
m,
x1x2=-2m,
∴(
 m)2+8m=25,
m)2+8m=25,整理得出:
9m 2+32m-100=0,
(9m+50)(m-2)=0,
解得:m1=-
 ,m2=2,
,m2=2,当m1=-
 时,△<0,故舍去,
时,△<0,故舍去,当m2=2时,△>0,
∴方程为:x2-3x-4=0,
解得:x1=-1,x2=4;
(2)∵如图所示,x1=-1,x2=4,CO=2,
∴AO=1,OB=4,DO=CO=2,
∵AD2=AO2+DO2=1+4=5,BD2=DO2+BO2=4+16=20,
AB 2=25,
∴AD2+BD2=AB 2,
∴AD⊥BD,
如图所示这样的D点有2个.
点评:此题主要考查了根与系数的关系以及勾股定理和十字相乘法解一元二次方程,将根与系数的关系与代数式相结合解题是一种经常使用的解题方法.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 数形结合的思想方法
数形结合的思想方法