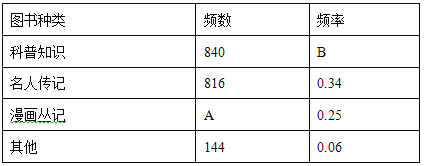
��Ŀ����
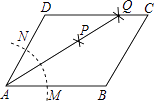
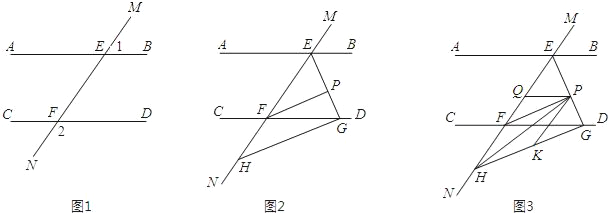
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
��1�����ж�ֱ��AB��ֱ��CD��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN��һ�㣬��GH��EG����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ��ʹ��PHK����HPK����PQƽ�֡�EPK���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�
���𰸡���1��֤������������2��֤������������3��45��
��������
���⣨1�����öԶ�����ȡ���������������֪ͬ���ڽǡ�AEF����CFE������������֤AB��CD��
��2�����ã�1����ƽ���ߵ�������֪�㣻Ȼ����ݽ�ƽ���ߵ����ʡ��������ڽǺͶ���֤�á�EPF=90�㣬��EG��PF���ʽ����֪����GH��EG����֤PF��GH��
��3��������������Ƕ������������ڽǺͶ�����á�4=90��-��3=90��-2��2��Ȼ�����ڲ��ǵĶ��塢��ƽ���ߵĶ�����֪��QPK=![]() ��EPK=45��+��2��������ͼ���еĽ���Ǽ�ĺͲ��ϵ��á�HPQ�Ĵ�С���䣬�Ƕ�ֵ45�㣮
��EPK=45��+��2��������ͼ���еĽ���Ǽ�ĺͲ��ϵ��á�HPQ�Ĵ�С���䣬�Ƕ�ֵ45�㣮
�����������1����ͼ1��

�ߡ�1���2������
���1+��2=180�㣮
�֡ߡ�1=��AEF����2=��CFE��
���AEF+��CFE=180�㣬
��AB��CD��
��2����ͼ2���ɣ�1��֪��AB��CD��
���BEF+��EFD=180�㣮
�֡ߡ�BEF���EFD�Ľ�ƽ���߽��ڵ�P��
���FEP+��EFP=![]() ����BEF+��EFD��=90�㣬
����BEF+��EFD��=90�㣬
���EPF=90�㣬��EG��PF��
��GH��EG��
��PF��GH��
��3����HPQ�Ĵ�С�������仯���������£�
��ͼ3���ߡ�1=��2��
���3=2��2��
�֡�GH��EG��
���4=90��-��3=90��-2��2��
���EPK=180��-��4=90��+2��2��
��PQƽ�֡�EPK��
���QPK=![]() ��EPK=45��+��2��
��EPK=45��+��2��
���HPQ=��QPK-��2=45�㣬
���HPQ�Ĵ�С�������仯��һֱ��45�㣮