题目内容
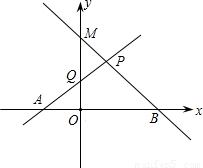
 如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.
如图,已知直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.(1)用m,n表示A、B、P点的坐标;
(2)若点Q是PA与y轴的交点,且P点坐标为(
| 1 |
| 3 |
| 4 |
| 3 |
分析:(1)直线PA的解析式令y=0求解即可得到点A的坐标,直线PB的解析式令y=0求解即可得到点B的坐标,联立两直线解析式求解即可得到点P的坐标;
(2)根据点P的坐标求出点A、B的坐标,再求出点Q的坐标,然后根据S四边形PQOB=S△PAB-S△AOQ列式计算即可得解.
(2)根据点P的坐标求出点A、B的坐标,再求出点Q的坐标,然后根据S四边形PQOB=S△PAB-S△AOQ列式计算即可得解.
解答:解:(1)令y=0,则x+n=0,
解得x=-n,
所以,点A(-n,0),
令y=0,则-2x+m=0,
解得x=
,
所以,点B(
,0),
联立
,
解得
,
所以,点P(
,
);
(2)∵P点坐标为(
,
),
∴
,
解得
,
直线PA的解析式令x=0,则y=n=1,
S四边形PQOB=S△PAB-S△AOQ,
=
×(2+1)×
-
×1×1,
=
.
解得x=-n,
所以,点A(-n,0),
令y=0,则-2x+m=0,
解得x=
| m |
| 2 |
所以,点B(
| m |
| 2 |
联立
|
解得
|
所以,点P(
| m-n |
| 3 |
| m+2n |
| 3 |
(2)∵P点坐标为(
| 1 |
| 3 |
| 4 |
| 3 |
∴
|
解得
|
直线PA的解析式令x=0,则y=n=1,
S四边形PQOB=S△PAB-S△AOQ,
=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
=
| 3 |
| 2 |
点评:本题考查了两直线相交的问题,主要利用了直线与坐标轴的交点坐标的求法,两直线交点的求法,(2)观察出四边形的面积等于两个三角形的面积的差是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 m>n)的图象.
m>n)的图象.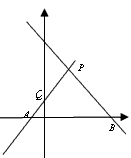
 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式。 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.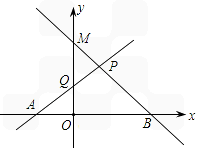
 ,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.
,AB=2,试求出点P的坐标,并求出直线PA与PB的表达式.