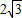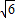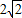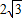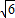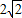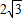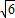Question

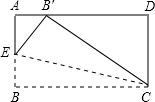
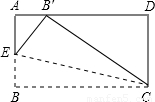
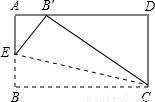
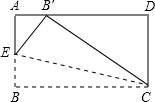如图一块矩形的纸片CD=2cm，如果沿图中的EC对折，B点刚好落在AD上，此时∠BCE=15°，则BC的长为（　　）cm．

• A、4
• B、2

  3

• C、

  6

• D、2

  2

Answer 1

分析：由折叠可知∠BCB'=2∠BCE=30°，根据矩形的性质BC∥AD和Rt△B'CD中的B'C=2CD=4，可求得BC的长．

解答：解：∵△EB′C是△EBC翻折后得到的
∴∠BCB'=2∠BCE=30°
∵BC∥AD
∴∠CB'D=∠BCB'=30°
在Rt△B'CD中，B'C=2CD=4
∴BC=B'C=4．
故选A．

点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等，对应线段相等．