��Ŀ����
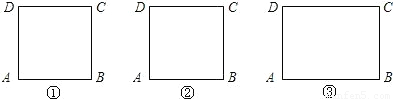
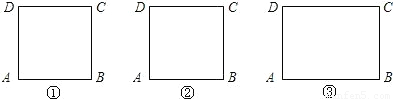
����̽������1������ͼ�ٵ�������ABCD�ڣ�����ʹ��APB=90���һ���㣬��˵�����ɣ�
��2������ͼ�ڵ�������ABCD�ڣ����ߣ�������ʹ��APB=60������еĵ�P����˵�����ɣ�
��������
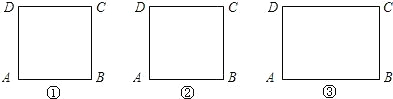
��3����ͼ�ۣ�����һ����θְ�ABCD��AB=4��BC=3������ʦ���������ó�����ȫ�ȵġ�������ġ�APB�͡�CP��D�ְ壬�ҡ�APB=��CP'D=60�ȣ�������ͼ���л�������Ҫ��ĵ��P��P�䣬�������APB�����������������ţ���
��������1����Ϊ�����εĶԽ����ഹֱ����������AC��BD���ڵ�O��O��Ϊ����
��2������ABΪ���������������ȱߡ�ABP��������ABP�����ԲO���ֱ���AD��BC���ڵ�E��F����Ϊ��ԲO�У���AB���Ե�
�ϵ�Բ�ܽǾ�Ϊ60�㣬����
�ϵ����е��Ϊ����ĵ�P��
��3����Ϊ��APB=��CP'D=60�㣬��APB�͡�CP��D������������ͬ��2����
������AC��
����ABΪ�����ȱߡ�ABE��
�����ȱߡ�ABE�����ԲO����AC�ڵ�P��
����AC�Ͻ�ȡAP'=CP�����P��P��Ϊ����
Ҫ���APB��������ɹ���B��BG��AC����AC�ڵ�G��
��Ϊ��Rt��ABC�У�AB=4��BC=3�����ù��ɶ�������AC=5�����������ε��������BG=
=
��������Rt��ABG�У�AB=4���������ù��ɶ��������AG��ֵ��Ȼ����Rt��BPG�У���Ϊ��BPA=60�㣬����PG=
=
��
=
����AP=AG+PG��S��APB=
AP•BG����������𰸣�
��2������ABΪ���������������ȱߡ�ABP��������ABP�����ԲO���ֱ���AD��BC���ڵ�E��F����Ϊ��ԲO�У���AB���Ե�
 |
| APB |
 |
| EF |
��3����Ϊ��APB=��CP'D=60�㣬��APB�͡�CP��D������������ͬ��2����
������AC��
����ABΪ�����ȱߡ�ABE��
�����ȱߡ�ABE�����ԲO����AC�ڵ�P��
����AC�Ͻ�ȡAP'=CP�����P��P��Ϊ����
Ҫ���APB��������ɹ���B��BG��AC����AC�ڵ�G��
��Ϊ��Rt��ABC�У�AB=4��BC=3�����ù��ɶ�������AC=5�����������ε��������BG=
| AB•BC |
| AC |
| 12 |
| 5 |
| BG |
| tan60�� |
| 12 |
| 5 |
| ||
| 3 |
4
| ||
| 5 |
| 1 |
| 2 |
���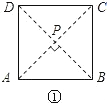 �⣺��1����ͼ�٣�����AC��BD���ڵ�P��
�⣺��1����ͼ�٣�����AC��BD���ڵ�P��
���APB=90�ȣ����PΪ����3�֣�
��2����ͼ�ڣ��������£�
����ABΪ���������������ȱߡ�ABP��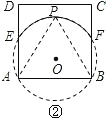
������ABP�����ԲO���ֱ���AD��BC���ڵ�E��F��
����ԲO�У���AB���Ե�
�ϵ�Բ�ܽǾ�Ϊ60�㣬
��
�ϵ����е��Ϊ����ĵ�P����7�֣�
��3����ͼ�ۣ��������£�
������AC��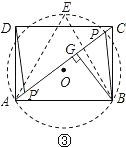
����ABΪ�����ȱߡ�ABE��
�����ȱߡ�ABE�����ԲO����AC�ڵ�P��
����AC�Ͻ�ȡAP'=CP�����P��P��Ϊ����9�֣�
������ʱ����ͼȷ�������IJ��۷֣�
����B��BG��AC����AC�ڵ�G��
����Rt��ABC��AB=4��BC=3��
��AC=
=5��
��BG=
=
����10�֣�
��Rt��ABG��AB=4��
��AG=
=
����Rt��BPG�У���BPA=60�㣬
��PG=
=
��
=
��
��AP=AG+PG=
+
��
��S��APB=
AP•BG=
��(
+
)��
=
����12�֣�
 �⣺��1����ͼ�٣�����AC��BD���ڵ�P��
�⣺��1����ͼ�٣�����AC��BD���ڵ�P�����APB=90�ȣ����PΪ����3�֣�
��2����ͼ�ڣ��������£�
����ABΪ���������������ȱߡ�ABP��

������ABP�����ԲO���ֱ���AD��BC���ڵ�E��F��
����ԲO�У���AB���Ե�
 |
| APB |
��
 |
| EF |
��3����ͼ�ۣ��������£�
������AC��

����ABΪ�����ȱߡ�ABE��
�����ȱߡ�ABE�����ԲO����AC�ڵ�P��
����AC�Ͻ�ȡAP'=CP�����P��P��Ϊ����9�֣�
������ʱ����ͼȷ�������IJ��۷֣�
����B��BG��AC����AC�ڵ�G��
����Rt��ABC��AB=4��BC=3��
��AC=
| AB2+BC2 |
��BG=
| AB•BC |
| AC |
| 12 |
| 5 |
��Rt��ABG��AB=4��
��AG=
| AB2-BG2 |
| 16 |
| 5 |
��PG=
| BG |
| tan60�� |
| 12 |
| 5 |
| ||
| 3 |
4
| ||
| 5 |
��AP=AG+PG=
| 16 |
| 5 |
4
| ||
| 5 |
��S��APB=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 5 |
4
| ||
| 5 |
| 12 |
| 5 |
96+24
| ||
| 25 |
��������������ϸ�������⣬����ͬ�����Ե�Բ�ܽ���ȼ��ɽ�����⣮

��ϰ��ϵ�д�
�����Ŀ