题目内容
半径分别为13和15的两圆相交,且公共弦长为24,则两圆的圆心距为
- A.
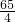 或14
或14 - B.
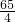 或4
或4 - C.14
- D.4或14
D
分析:利用了连心线垂直平分公共弦,勾股定理求解,注意两圆相交的情况有两种情况.
解答:
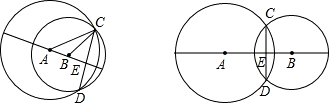
如图,圆A与圆B相交于点C,D,CD与AB交于点E,AC=15,BC=13,
由于连心线AB垂直平分CD,有CE=12,△ACE,△BCE是直角三角形,
由勾股定理得,AE=9,BE=5,
而两圆相交的情况有两种,当为左图时,AB=AE-BE=9-5=4,
当为右图时,AB=AE+BE=14.
故选D.
点评:本题利用了连心线垂直平分公共弦,勾股定理.
分析:利用了连心线垂直平分公共弦,勾股定理求解,注意两圆相交的情况有两种情况.
解答:

如图,圆A与圆B相交于点C,D,CD与AB交于点E,AC=15,BC=13,
由于连心线AB垂直平分CD,有CE=12,△ACE,△BCE是直角三角形,
由勾股定理得,AE=9,BE=5,
而两圆相交的情况有两种,当为左图时,AB=AE-BE=9-5=4,
当为右图时,AB=AE+BE=14.
故选D.
点评:本题利用了连心线垂直平分公共弦,勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
半径分别为13和15的两圆相交,且公共弦长为24,则两圆的圆心距为( )
A、
| ||
B、
| ||
| C、14 | ||
| D、4或14 |
 或14
或14 或4
或4 或14
或14 或4
或4 或14
或14 或4
或4