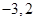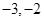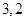题目内容
如图,矩形OABC的顶点A、C分别在x轴、y轴正半轴上,B点坐标为(3,2),OB与AC交于点P,D、E、F、G分别是线段OP、AP、BP、CP的中点,则四边形DEFG的周长为 ▲ .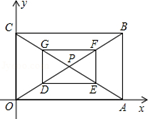

5
坐标与图形性质,矩形的性质,三角形中位线定理。
【分析】根据题意,由B点坐标知OA=BC=3,AB=OC=2;根据三角形中位线定理可求四边形DEFG的各边长度,从而求周长:
∵四边形OABC是矩形,∴OA=BC,AB=OC, BA⊥OA,BC⊥OC。
∵B点坐标为(3,2),∴OA=3,AB=2。
∵D、E、F、G分别是线段OP、AP、BP、CP的中点,∴DE=GF=1.5; EF=DG=1。
∴四边形DEFG的周长为 (1.5+1)×2=5。
【分析】根据题意,由B点坐标知OA=BC=3,AB=OC=2;根据三角形中位线定理可求四边形DEFG的各边长度,从而求周长:
∵四边形OABC是矩形,∴OA=BC,AB=OC, BA⊥OA,BC⊥OC。
∵B点坐标为(3,2),∴OA=3,AB=2。
∵D、E、F、G分别是线段OP、AP、BP、CP的中点,∴DE=GF=1.5; EF=DG=1。
∴四边形DEFG的周长为 (1.5+1)×2=5。

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
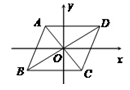

 关于原点对称的点的坐标是 。
关于原点对称的点的坐标是 。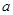 ,-l),与点B(4,
,-l),与点B(4,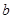 )关于
)关于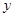 轴对称,则
轴对称,则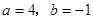
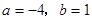
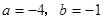
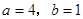
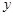 轴向上平移5个单位,再沿
轴向上平移5个单位,再沿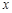 轴向左平移4个单位得到点A′,则点A′的坐标是 .
轴向左平移4个单位得到点A′,则点A′的坐标是 . 与点
与点 关于
关于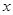 轴对称,则
轴对称,则 的值分别是( )
的值分别是( )