Question

如图，AB是⊙O的直径，C、D是AB的三等分点，如果⊙O的半径为1，P是线段AB上的任意一点，则图中阴影部分的面积为（　　）

• A、

  π

  3

• B、

  π

  6

• C、

  π

  2

• D、

  2π

  3

Answer 1

分析：连接CD、OC、OD；根据题意，得CD∥AB．那么△CPD与△OCD同底等高，因此△CPD的面积等于△OCD的面积．
则阴影部分的面积=半圆的面积-扇形OCD的面积=

π

2

-

π

6

=

π

3

．

解答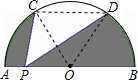：解：连接OC、CD、OD，则CD∥AB．
∴S_△CPD=S_△OCD；
因此S_阴影=S_半圆-S_扇形OCD
=

1

2

×π×1²-

60π×12

360

，
=

π

2

-

π

6

=

π

3

．
故选A．

点评：本题中能够将不规则图形的面积进行转换成规则图形的面积是解题的关键．