题目内容
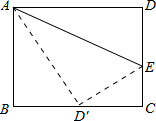如图，一个长方形的ABCD长为8cm，宽为6cm，E为边CD上的一点，现把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处．（1）请说明Rt△ABD′与Rt△ECD′相似；
（2）求CE的长．
分析：（1）根据长方形的性质和折叠推出∠D=∠D'=90°，AD=AD'=8，AB=DC=6，DE=D'E，∠B=∠C=90°，求出∠BAD'=∠ED'C即可；
（2）设CE=x，DE=ED'=6-x，根据勾股定理求出BD'，在△CD'E中，根据勾股定理得到x的方程，求出方程的解即可．
（2）设CE=x，DE=ED'=6-x，根据勾股定理求出BD'，在△CD'E中，根据勾股定理得到x的方程，求出方程的解即可．
解答：解：（1）证明：∵长方形的ABCD，把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处．
∴∠D=∠D'=90°，AD=AD'=8，AB=DC=6，DE=D'E，∠B=∠C=90°，
∴∠BAD'+∠AD'B=90°，∠AD'B+∠ED'C=90°，
∴∠BAD'=∠ED'C，
∴Rt△ABD'∽Rt△ECD'．
（2）设CE=x，DE=ED'=6-x，
在△ABD'中，由勾股定理得：BD'=
=2
，
∴CD'=8-2
，
在△CD'E中，由勾股定理得：CD'2+CE2=D'E2，
代入求出x=
，
CE=
．
∴∠D=∠D'=90°，AD=AD'=8，AB=DC=6，DE=D'E，∠B=∠C=90°，
∴∠BAD'+∠AD'B=90°，∠AD'B+∠ED'C=90°，
∴∠BAD'=∠ED'C，
∴Rt△ABD'∽Rt△ECD'．
（2）设CE=x，DE=ED'=6-x，
在△ABD'中，由勾股定理得：BD'=
| AD′2-AB2 |
| 7 |
∴CD'=8-2
| 7 |
在△CD'E中，由勾股定理得：CD'2+CE2=D'E2，
代入求出x=
8
| ||
| 3 |
CE=
8
| ||
| 3 |
点评：本题主要考查对矩形的性质，相似三角形的性质和判定，折叠问题，勾股定理等知识点的理解和掌握，能综合运用性质进行推理是解此题的关键．
练习册系列答案
相关题目
如图是一个长方形的铝合金窗框，其长为a（m），高为b（m），装有同样大的塑钢玻璃，当第②块向右拉到与第③块重叠| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，一个长方形的运动场，有一个球落到了点C，小明要从点A走到点C捡球，至少要走多少米？
12、如图是一个长方形的土地，长50m，宽48m．由南到北，由东到西各修筑一条同样宽度的彩石路，要使空地的面积是2208m2，如果设小路宽为xm，根据题意所列的方程为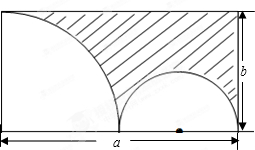
如图，一个长方形的长为a，宽为b，