题目内容
已知AB是⊙O的一条弦,P是⊙O外一点,PB切⊙O于B,PA交⊙O于C,且AC=BC,PD⊥AB于D,E是AB的中点,DE=2006.则PB的值为
- A.1003
- B.2006
- C.4012
- D.8024
C
分析:连接OB.设OE=a,EB=x,OB=m.根据相似三角形的性质得比例线段,建立相关线段的关系后求解.
解答: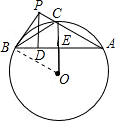 解:连接OB.
解:连接OB.
设OE=a,EB=x,OB=m.
△AEC与△ADP相似,有:x:(x+2006)=(a+m):DP;
△EBO与△BDP相似,有:x:DP=a:(2006-x);
a2+x2=m2故x2=(m-a)(m+a).
三式联立得:(2006-x):(2006+x)=a:(m-a),
可化为:(2006-x):4012=a:m.
在相似三角形EOB与DBP中(2006-x):BP=a:m,
所以BP=4012.
故选C.
点评:本题主要考查了切线的性质,垂径定理,相似三角形等知识点,用相似三角形得出线段之间的比例关系是解题的关键.
分析:连接OB.设OE=a,EB=x,OB=m.根据相似三角形的性质得比例线段,建立相关线段的关系后求解.
解答:
 解:连接OB.
解:连接OB.设OE=a,EB=x,OB=m.
△AEC与△ADP相似,有:x:(x+2006)=(a+m):DP;
△EBO与△BDP相似,有:x:DP=a:(2006-x);
a2+x2=m2故x2=(m-a)(m+a).
三式联立得:(2006-x):(2006+x)=a:(m-a),
可化为:(2006-x):4012=a:m.
在相似三角形EOB与DBP中(2006-x):BP=a:m,
所以BP=4012.
故选C.
点评:本题主要考查了切线的性质,垂径定理,相似三角形等知识点,用相似三角形得出线段之间的比例关系是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知AB是⊙O的一条弦,P是⊙O外一点,PB切⊙O于B,PA交⊙O于C,且AC=BC,PD⊥AB于D,E是AB的中点,DE=2008.则PB的值为( )
| A、1004 | B、2008 | C、4016 | D、8032 |
 (2012•峨眉山市模拟)如图,已知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD=
(2012•峨眉山市模拟)如图,已知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD=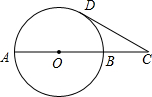 (2012•黑龙江)如图,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切,切点为D,若CD=
(2012•黑龙江)如图,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切,切点为D,若CD=