题目内容

如图，某天晚8点时，一台风中心位于点O正北方向160千米点A处，台风中心以每小时20千米的速度向东南方向移动，在距台风中心小于等于120千米的范围内将受到台风影响，同时在点O有一辆汽车以每小时40千米的速度向东行驶．
（1）汽车行驶了多少时间后受到台风的影响？
（2）汽车受到台风影响的时间有多少？

解：以O为原点，OA所在直线为y轴，汽车行驶的路线为x轴，作出坐标系．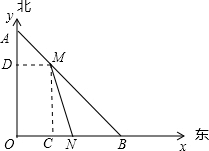

设当台风中心在M点，汽车在N点开始，汽车受到影响，设运动时间是t小时，过M作MC⊥x轴与C，作MD⊥y轴．
则△ADM是等腰直角三角形，AM=20t，则AD=DM= $\text{[math]}$ AM=10 $\text{[math]}$ t，
因而M的坐标是：（10 $\text{[math]}$ t，160-10 $\text{[math]}$ t），
N的坐标是：（40t，0）．
汽车受到影响，则MN=120千米，
即（40t-10 $\text{[math]}$ t）²+（160-10 $\text{[math]}$ t）²=120²，
即（20-8 $\text{[math]}$ ）t²-32 $\text{[math]}$ t+112=0，
△=3584 $\text{[math]}$ -6912＜0，
则方程无解，即汽车不受影响．
故（1）（2）都无解．
分析：以O为原点，OA所在直线为y轴，汽车行驶的路线为x轴，作出坐标系，设当台风中心在M点，汽车在N点开始，汽车受到影响，设运动时间是t小时，即可利用t表示出M、N的坐标，根据MN=120，即可得到一个关于t的方程，解方程即可求得t的值．
点评：本题考查了勾股定理，把判断是否受影响的问题转化成一元二次方程的解得问题是关键．