题目内容
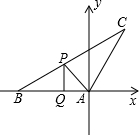 (2013•唐山一模)如图,△ABC中,P是BC上一点,PQ⊥AB,垂足为Q,PQ=10,∠B=30°,∠PAB=45°,以A为原点,AB所在的直线为x轴建立如图所示的坐标系.
(2013•唐山一模)如图,△ABC中,P是BC上一点,PQ⊥AB,垂足为Q,PQ=10,∠B=30°,∠PAB=45°,以A为原点,AB所在的直线为x轴建立如图所示的坐标系.(1)点B的坐标为
(-10-10
,0)
| 3 |
(-10-10
,0)
,点P的坐标为| 3 |
(-10,10)
(-10,10)
.(2)如果AC与x轴的正半轴的夹角为75°,求AC的长.
分析:(1)在Rt△PQB中求出BQ,在Rt△PQA中求出AQ,即可得出点B及点P的坐标;
(2)先判定△APQ是等腰直角三角形,然后求出PA的长,再求出PB的长,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C=45°,然后求出△BAP和△BAC相似,再根据相似三角形对应边成比例列式计算即可求出AC的长.
(2)先判定△APQ是等腰直角三角形,然后求出PA的长,再求出PB的长,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C=45°,然后求出△BAP和△BAC相似,再根据相似三角形对应边成比例列式计算即可求出AC的长.
解答:解:(1)在Rt△PQB中,∠B=30°,PQ=10,
则BQ=10
,
在Rt△PQA中,PQ=10,∠PAB=45°,
则AQ=PQ=10,
故可得点B的坐标为(-10-10
,0),点P的坐标为(-10,10);
(2)∵PQ⊥AB,∠PAB=45°,
∴△APQ是等腰直角三角形,
∵PQ=10,
∴PA=10
,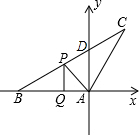
∵∠B=30°,
∴PB=2PQ=20,
∵∠B=30°,AC与x轴的正半轴的夹角为75°,
∴∠C=75°-30°=45°,
∴∠C=∠PAB=45°,
又∵∠B=∠B=30°,
∴△BAP∽△BAC,
∴
=
,
即
=
,
解得AC=
(5+5
)=5
+5
,
所以,AC的长为5
+5
.
则BQ=10
| 3 |
在Rt△PQA中,PQ=10,∠PAB=45°,
则AQ=PQ=10,
故可得点B的坐标为(-10-10
| 3 |
(2)∵PQ⊥AB,∠PAB=45°,
∴△APQ是等腰直角三角形,
∵PQ=10,
∴PA=10
| 2 |

∵∠B=30°,
∴PB=2PQ=20,
∵∠B=30°,AC与x轴的正半轴的夹角为75°,
∴∠C=75°-30°=45°,
∴∠C=∠PAB=45°,
又∵∠B=∠B=30°,
∴△BAP∽△BAC,
∴
| AP |
| AC |
| PB |
| AB |
即
10
| ||
| AC |
| 20 | ||
10+10
|
解得AC=
| 2 |
| 3 |
| 2 |
| 6 |
所以,AC的长为5
| 2 |
| 6 |
点评:本题考查了解直角三角形、等腰直角三角形的判定与性质,综合性较强,难点在第二问,关键在于利用外角的性质判断出∠B=∠C.

练习册系列答案
相关题目
 (2013•唐山一模)如图,给出下列四组条件:
(2013•唐山一模)如图,给出下列四组条件: