题目内容
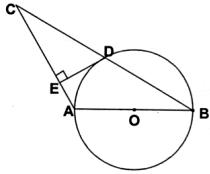
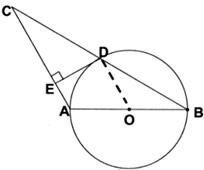
(本题满分l2分)⊙O直径AB=4,∠ABC=30°,BC=4 。D是线段BC中点,
。D是线段BC中点,
【小题1】(1)试判断D与⊙O的位置关系并说明理由;
【小题2】(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O切线。
【小题1】(1)答:点D在⊙O上…………1分
设线段BC和⊙O交于D’,连接AD;
∵AB是⊙O的直径
∴∠AD’B=90°…………2分
∵∠ABC=30°
∴AD’=
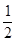 AB=
AB=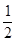 ×4=2…………3分
×4=2…………3分在Rt△ABD’中
BD’=
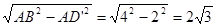 …………4分
…………4分∵D是线段BC中点
∴BD’=
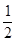 BC=
BC=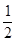 ×4
×4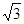 =2
=2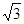 ……5分
……5分∴BD’=BD
即点D、D’重合
∴点D在⊙O上
【小题2】(2)连接OD
∵DE⊥AC
∴∠DEC=90°…………7分
∵D是线段BC中点,O是直径AB中点
∴OD是△ABC的中位线
∴OD∥AC…………9分
∴∠ODE=∠DEC=90°
∴DE⊥OD…………11分
∴直线DE是⊙O切线…………l2分
 解析:
解析:略

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 (
( (元)之间的函数关系式.
(元)之间的函数关系式. (
( (元)之间的函数关系式.
(元)之间的函数关系式.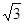 。D是线段BC中点,
。D是线段BC中点,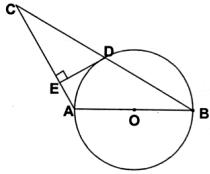
 (
( (元)之间的函数关系式.
(元)之间的函数关系式.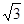 。D是线段BC中点,
。D是线段BC中点,