题目内容
如11图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C
(1) 求证:△ABF∽△EAD
(2)  若AB=4,S ABCD=
若AB=4,S ABCD=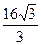 ,求AE的长
,求AE的长
(3) 在(1)、(2)条件下,若AD=3,求BF的长(计算结果可含根号)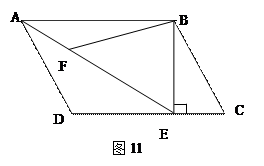
证明:(1)∵四边形ABCD
为平行四边形,∴∠BAF=∠AED
∠C+∠D=180°,∴∠C=∠BFE,∠BFE+∠BFA=180°,∴∠D=∠BFA
∴△ABF∽△EAD (2)解:∵S ABCD=
(2)解:∵S ABCD=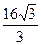 ,∴AB·BE=
,∴AB·BE=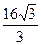 ,∵AB=4
,∵AB=4
∴BE= ∴AE2=AB2+BE2=42+(
∴AE2=AB2+BE2=42+( )2 AE=
)2 AE=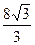
(3)解:由(1)有 =
=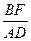 ,又AD=3,∴BF=
,又AD=3,∴BF=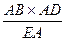 =4×3×
=4×3× =
=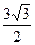
解析

练习册系列答案
相关题目