题目内容
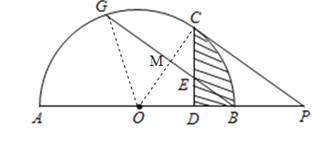
【题目】如图,AB是⊙O的直径,C是![]() 的中点,点P在AB的延长线上,且PC与⊙O相切于点C,过点C作CD⊥AB,垂足为D,CD 与BG交于E.
的中点,点P在AB的延长线上,且PC与⊙O相切于点C,过点C作CD⊥AB,垂足为D,CD 与BG交于E.
(1)求证:①PC//BG;②![]() ;
;
(2)若弧AG的度数为60°,且⊙O的半径为2,试求阴影部分的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)①连接OG,OC.可以得出OM⊥BG, OC⊥PC,从而可以得出结论;
②由垂径定理得到BM=GM=![]() BG,再证明△COD≌△BOM,即可得到结论;
BG,再证明△COD≌△BOM,即可得到结论;
(2)由弧AG=60°,得到∠COD=60°,∠OCD=30°,从而得到OD,CD的长,由![]() 即可得到结论.
即可得到结论.
试题解析:解:(1)①连接OG,OC.∵弧CG=弧BC,∴∠GOC=∠COB,∵OC=OB,∴OM⊥BG.∵PC与⊙O相切于点C,∴OC⊥PC,∴PC∥BG;
②∵OM⊥BG,∴BM=GM=![]() BG.在△COD和△BOM中,∵∠COD=∠BOM,∠CDO=∠BMO=90°,OC=OB,∴△COD≌△BOM,∴CD=BM,∴CD=
BG.在△COD和△BOM中,∵∠COD=∠BOM,∠CDO=∠BMO=90°,OC=OB,∴△COD≌△BOM,∴CD=BM,∴CD=![]() BG;
BG;
(2)∵弧AG=60°,∴弧GB=120°,∴弧BC=60°,∴∠COD=60°,∴∠OCD=30°.∵OC=2,∴OD=1,CD=![]() ,∴
,∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

