Question

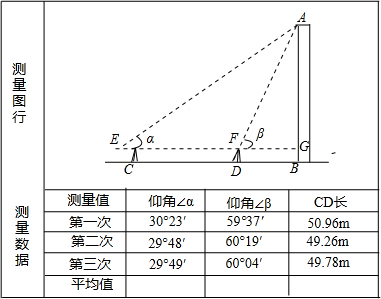
下表是育英中学数学课外小组测量建筑物AB的高度实验报告的部分内容：

（1）完成上表中的平均值数据，将结果填在表格中；
（2）若测量仪器高度EC=FD=1.52m，根据表格提供的数据计算建筑物AB的高度．（取1.732，结果精确到0.01米）

Answer 1

【答案】分析：（1）把相应的值相加后除以3即可；
（2）易得AF=EF=CD，利用∠β的正弦值可得AG的值，加上测量仪器高度即为AB的高度．
解答：解：（1）

平均值

30°

60°

50m

（2）在△AEF中，∠EAF=∠β-∠α=60°-30°=30°
∴∠EAF=∠α，
∴AF=EF=CD=50m．
在△AFG中，∵sinβ=
∴AG=AF×sin60°
=50×=25
≈43.30（m）
AB=AG+BG=AG+CE=43.30+1.52=44.82（m）
答：建筑物AB的高度约为44.82米．
点评：考查解直角三角形的应用；利用等角对等边得到AF的值是解决本题的突破点．