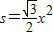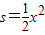题目内容
 (2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.
(2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.(1)求证:∠AED=∠ADC,∠DEC=∠B;
(2)求证:AB2=AE•AC.
【答案】分析:(1)根据三角形的内角和定理可证∠AED=∠ADC,∠DEC=∠B;
(2)根据相似三角形的判定,由AA可证△ADE∽△ACD,得到 ,即AD2=AE•AC.又AB=AD,即证AB2=AE•AC.
,即AD2=AE•AC.又AB=AD,即证AB2=AE•AC.
解答:证明:(1)在△ADE和△ACD中,
∵∠ADE=∠C,∠DAE=∠DAE,
∴∠AED=180°-∠DAE-∠ADE,
∠ADC=180°-∠DAE-∠C,
∴∠AED=∠ADC.(2分)
∵∠AED+∠DEC=180°,
∠ADB+∠ADC=180°,
∴∠DEC=∠ADB,
又∵AB=AD,
∴∠ADB=∠B,
∴∠DEC=∠B.(4分)
(2)在△ADE和△ACD中,
由(1)知∠ADE=∠C,∠AED=∠ADC,
∴△ADE∽△ACD,(5分)
∴ ,
,
即AD2=AE•AC.(7分)
又AB=AD,
∴AB2=AE•AC.(8分)
点评:本题考查了三角形的内角和定理,等腰三角形的性质,相似三角形的判定等知识点,难度适中.
(2)根据相似三角形的判定,由AA可证△ADE∽△ACD,得到
 ,即AD2=AE•AC.又AB=AD,即证AB2=AE•AC.
,即AD2=AE•AC.又AB=AD,即证AB2=AE•AC.解答:证明:(1)在△ADE和△ACD中,
∵∠ADE=∠C,∠DAE=∠DAE,
∴∠AED=180°-∠DAE-∠ADE,
∠ADC=180°-∠DAE-∠C,
∴∠AED=∠ADC.(2分)
∵∠AED+∠DEC=180°,
∠ADB+∠ADC=180°,
∴∠DEC=∠ADB,
又∵AB=AD,
∴∠ADB=∠B,
∴∠DEC=∠B.(4分)
(2)在△ADE和△ACD中,
由(1)知∠ADE=∠C,∠AED=∠ADC,
∴△ADE∽△ACD,(5分)
∴
 ,
,即AD2=AE•AC.(7分)
又AB=AD,
∴AB2=AE•AC.(8分)
点评:本题考查了三角形的内角和定理,等腰三角形的性质,相似三角形的判定等知识点,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
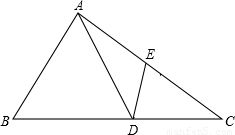 (2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.
(2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.




 (2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.
(2010•泰安)如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.