题目内容
【题目】如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.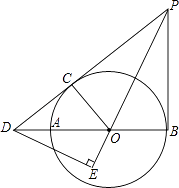
(1)求证:PB是⊙O的切线;
(2)若PB=9,DB=12,求⊙O的半径.
【答案】
(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线
(2)解:在Rt△PBD中,PB=9,DB=12,
根据勾股定理得:PD= ![]() =15,
=15,
∵PD与PB都为圆的切线,
∴PC=PB=9,
∴DC=PD﹣PC=15﹣9=6,
在Rt△CDO中,设OC=r,则有DO=12﹣r,
根据勾股定理得:(12﹣r)2=r2+62,
解得:r=4.5,
则圆的半径为4.5
【解析】(1)由已知在△DEO和△PBO中,∠EDB=∠EPB及对顶角相等,得出∠OBP=∠E,再根据垂直的定义证得∠OBP是直角,即可得证。
(2)先在Rt△PBD中根据勾股定理求出PD的长,再根据切线长定理得出PC=PB,再转化到Rt△CDO中根据勾股定理建立方程,即可求出圆的半径。
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目