Question

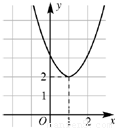
用“¤”定义一种运算：对于任意实数m、n和抛物线y=ax²，当y=ax²¤（m，n）后都可得到y=a（x-m）²+n．例如：当y=3x²¤（2，4）后得到y=3（x-2）²+4．当函数y=x²¤（1，n）后得到了新函数的图象（如图所示），则n=    ．

Answer 1

【答案】分析：抛物线的平移，实际上就是顶点的平移，根据新定义运算，得出顶点的变换规律，结合图形可求n的值．
解答：解：依题意可知抛物线顶点的变换规律，
而原抛物线解析式为y=x²，由图象可知新抛物线解析式为y=（x-1）²+2，
即顶点坐标为（1，2），则n=2．
故答案为：2．
点评：本题考查了抛物线的平移变换．关键是将抛物线的平移转化为顶点的平移，运用顶点式求抛物线解析式．