题目内容
 (2012•沈河区模拟)如图,△ABC内接于⊙O,D是
(2012•沈河区模拟)如图,△ABC内接于⊙O,D是 | BC |
(1)求证:EM=EN;
(2)已知:AB=5cm,AC=3cm,求AN的长;
(3)在(2)的条件下,若DE平分AB,求sin∠DEM的值.
分析:(1)连BE、EC、AE,根据D是
的中点,DE为直径,可得出点E是
的中点,所以
=
,再由四边形AEBC是圆内接四边形可得出∠EAN=∠CBE=∠BAE,根据AAS定理可知△AEM≌△AEN,故可得出结论;
(2))根据(1)中△AEM≌△AEN,得出EM=EN,AN=AM,故
=
,BE=CE,再由HL定力得出Rt△BME≌Rt△CNE,故BM=CN,即AB-AM=AB-AN=AC+AN,AN=
,由此即可得出结论;
(3))根据DE是直径可知当DE平分AB时,AB也是直径,故∠ACB=90°,设DE、BC交于点G,根据AAS定理得出△BOG≌△EOM,故∠ABC=∠DEM,sin∠DEM=sin∠ABC=
,由此即可得出结论.
 |
| BC |
 |
| BEC |
 |
| BE |
 |
| CE |
(2))根据(1)中△AEM≌△AEN,得出EM=EN,AN=AM,故
 |
| BE |
 |
| CE |
| AB-AC |
| 2 |
(3))根据DE是直径可知当DE平分AB时,AB也是直径,故∠ACB=90°,设DE、BC交于点G,根据AAS定理得出△BOG≌△EOM,故∠ABC=∠DEM,sin∠DEM=sin∠ABC=
| AC |
| AB |
解答: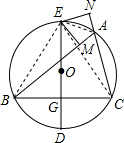 (1)证明:连BE、EC、AE,
(1)证明:连BE、EC、AE,
∵D是
的中点,DE为直径,
∴点E是
的中点,
∴
=
,
∵四边形AEBC是圆内接四边形,
∴∠EAN=∠CBE=∠BAE,
∵EM⊥AB于M,EN⊥AC于N,
∴∠AME=∠ANE=90°,
在△AEM与△AEN中,
,
∴△AEM≌△AEN(AAS),
∴EM=EN;
(2)∵由(1)知△AEM≌△AEN,
∴EM=EN,AN=AM,
∵
=
,
∴BE=CE,
在Rt△BME与Rt△CNE中,
,
∴Rt△BME≌Rt△CNE(HL),
∴BM=CN,即AB-AM=AB-AN=AC+AN,
∴AN=
=
=1cm;
(3)∵DE是直径,
∴当DE平分AB时,AB也是直径,
∴∠ACB=90°,
设DE、BC交于点G,
在△BOG与△EOM中,
,
∴△BOG≌△EOM(AAS),
∴∠ABC=∠DEM,
∴sin∠DEM=sin∠ABC=
=
.
 (1)证明:连BE、EC、AE,
(1)证明:连BE、EC、AE,∵D是
 |
| BC |
∴点E是
 |
| BEC |
∴
 |
| BE |
 |
| CE |
∵四边形AEBC是圆内接四边形,
∴∠EAN=∠CBE=∠BAE,
∵EM⊥AB于M,EN⊥AC于N,
∴∠AME=∠ANE=90°,
在△AEM与△AEN中,
|
∴△AEM≌△AEN(AAS),
∴EM=EN;
(2)∵由(1)知△AEM≌△AEN,
∴EM=EN,AN=AM,
∵
 |
| BE |
 |
| CE |
∴BE=CE,
在Rt△BME与Rt△CNE中,
|
∴Rt△BME≌Rt△CNE(HL),
∴BM=CN,即AB-AM=AB-AN=AC+AN,
∴AN=
| AB-AC |
| 2 |
| 5-3 |
| 2 |
(3)∵DE是直径,
∴当DE平分AB时,AB也是直径,
∴∠ACB=90°,
设DE、BC交于点G,
在△BOG与△EOM中,
|
∴△BOG≌△EOM(AAS),
∴∠ABC=∠DEM,
∴sin∠DEM=sin∠ABC=
| AC |
| AB |
| 3 |
| 5 |
点评:本题考查的是圆的综合题,涉及到圆内接四边形的性质、全等三角形的判定与性质、锐角三角函数的定义等知识,难度较大.

练习册系列答案
相关题目