题目内容
如图,⊙O中,两条弦AB、CD相交于P点,若PA=4,PB=3,PC=6,则CD的长为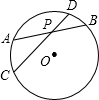
分析:根据相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”进行计算.
解答:解:由相交弦定理得:PA•PB=PC•PD,
∴DP=
=
=2,
∴CD=PC+PD=6+2=8.
∴DP=
| PA•PB |
| PC |
| 4×3 |
| 6 |
∴CD=PC+PD=6+2=8.
点评:本题主要考查相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”的应用.

练习册系列答案
相关题目




