题目内容
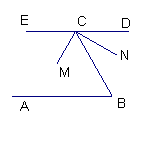
如图AB∥CD,∠NCM=90°,∠NCB=30°,CM平分∠BCE,求∠B的大小.

【答案】
60°
【解析】
试题分析:由CM平分∠BCE可得∠BCE=2∠BCM,由∠NCM=90°,∠NCB=30°可得∠BCM的度数,从而得到∠BCE的度数,再根据平行线的性质即得结果。
因为CM平分∠BCE,
所以∠BCE=2∠BCM.
因为∠NCM=90°,∠NCB=30°,
所以∠BCM=60°.
所以∠BCE=120°.
根据两直线平行,同旁内角互补,
因为AB∥CD,
所以∠BCE+∠B=180°.
所以∠B=60°.
考点:本题考查的是角平分线的性质,平行线的性质
点评:解答本题的关键是熟练掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目