题目内容
【题目】如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF. 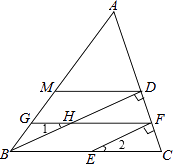
【答案】证明:∵BD⊥AC,EF⊥AC, ∴BD∥EF,
∴∠2=∠CBD,
∵∠2=∠1,
∴∠1=∠CBD,
∴GF∥BC,
∵BC∥DM,
∴MD∥GF,
∴∠AMD=∠AGF
【解析】由BD⊥AC,EF⊥AC,得到BD∥EF,根据平行线的性质得到∠2=∠CBD,等量代换得到∠1=∠CBD,根据平行线的判定定理得到GF∥BC,证得MD∥GF,根据平行线的性质即可得到结论.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示: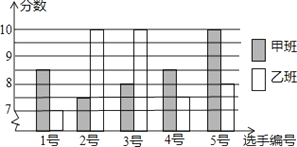
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?