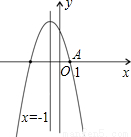题目内容
已知抛物线![]() 与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.
与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.

1.直接写出抛物线的对称轴,及抛物线与![]() 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
2.当∠ACB=90°时,求抛物线的解析式;
3.抛物线上是否存在点M,使得△ABM和△ABC的面积相等(△ABM与△ABC重合除外)?若存在,请直接写出点M坐标;若不存在,请说明理由.
4.在第一象限内,抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出这个最大值和点N坐标;若不存在,请说明理由.
1.对称轴是:直线x=1;点B的坐标是(3,0).…………………… 2分
2.由∠ACB=∠AOC=∠COB=90°得△AOC∽△COB,
∴![]() , ∴CO=
, ∴CO=![]() ,∴b=
,∴b=![]()
当![]() 时,
时,![]() ∴
∴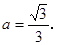 ………………… 4分
………………… 4分
∴![]()
3.点M的坐标是:(2,![]() ),(1+
),(1+![]() ,-
,-![]() )或(1-
)或(1-![]() ,-
,-![]() )………… 8分
)………… 8分
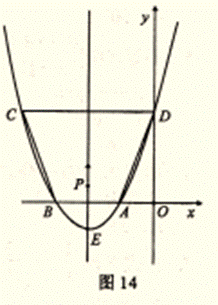
4.设点N的坐标为(m,n),则![]() ,
,
过点N作ND⊥AB于点D,则有:
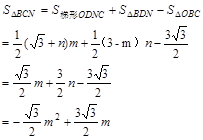
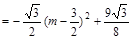 ……………………………… 10分
……………………………… 10分
∵![]() <0,
<0,
∴当![]() 时,△BCN的面积最大,最大值是
时,△BCN的面积最大,最大值是![]() ,
,
点N的坐标为![]() ……………………………… 12分
……………………………… 12分
解析:略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( ) 与x轴的一个交点为A(-1,0)
与x轴的一个交点为A(-1,0)