题目内容
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是 , Q点的坐标是 . 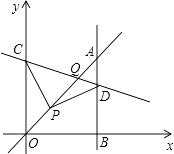
【答案】(0,4+2 ![]() );(2
);(2 ![]() +2,2
+2,2 ![]() +2)
+2)
【解析】解:过P点作x轴的平行线交y轴于M,交AB于N,如图,设P(0,t), ∴P(2,2),
∴OP=2 ![]() ,OM=BN=PM=2,CM=t﹣2,
,OM=BN=PM=2,CM=t﹣2,
∵线段PC绕点P顺时针旋转90°至线段PD,
∴PC=PD,∠CPD=90°,
∴∠CPM+∠DPN=90°,
而∠CPM+∠PCM=90°,
∴∠PCM=∠DPN,
在△PCM和△DPN中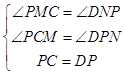 ,
,
∴△PCM≌△DPN,
∴PN=CM=2﹣t,DN=PM=2,
∴MN=2﹣t+2=t,DB=2+2=4,
∴D(t,4),
∵△OPC≌△ADP,
∴AD=OP=2 ![]() ,
,
∴A(t,4+2 ![]() ),
),
把A(t,4+2 ![]() )代入y=x得t=4+2
)代入y=x得t=4+2 ![]() ,
,
∴C(0,4+2 ![]() ),D(4+2
),D(4+2 ![]() ,4),
,4),
设直线CD的解析式为y=kx+b,
把C(0,4+2 ![]() ),D(4+2
),D(4+2 ![]() ,4)代入得
,4)代入得 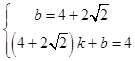 ,解得
,解得 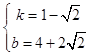 ,
,
∴直线CD的解析式为y=(1﹣ ![]() )x+4+2
)x+4+2 ![]() ,
,
解方程组 ![]() 得
得 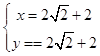 ,
,
∴Q(2 ![]() +2,2
+2,2 ![]() +2).
+2).
所以答案是(0,4+2 ![]() ),(2
),(2 ![]() +2,2
+2,2 ![]() +2).
+2).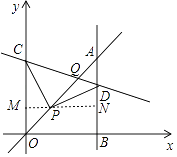
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目