题目内容
从A、B量水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各调查水14万吨,从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地50千米,设计一个调运方案使水的调运总量尽可能小.(1)设从A水库调往甲地的水量为x万吨,请你在下面表格空白处填上适当的数或式子.
| 地区 水库 | 甲 | 乙 | 总计 |
| A | x | ______ | 14 |
| B | ______ | ______ | 14 |
| 总计 | 15 | 13 | 28 |
(3)对于(2)中y与x的函数关系式,若求自变量的取值范围,应该列不等式组:______
【答案】分析:(1)通过设从A水库调往甲地的水量为x万吨,再根据各水库可调运的水量和甲乙两地需要的水量就可以表示出结论;
(2)根据影响水的调运量的两个因素通过(1)的代数式就可以求出调运总量为y万吨•千米与x之间的函数关系式;
(3)根据题意中的隐含条件和问题的实际意义建立不等式组求出其解就可以确定自变量的取值范围,再利用描点法就可以画出函数图象;
(4)由(2)的解析式和(3)的自变量的取值范围就可以最小调运量的方案.
解答:解:(1)设从A水库调往甲地的水量为x万吨,由题意得:
从A水库调往乙地的水量为:(14-x)吨,
从B水库调往甲地的水量为:(15-x)吨,
从B水库调往乙地的水量为:(x-1)吨,
故答案为:14-x,15-x,x-1;
(2)设水的调运总量为y万吨•千米,由题意,得
y=50x+30(14-x)+60(15-x)+50(x-1),
=10x+1270,
故答案为:10x+1270;
(3)由题意得:
 ,
,
解得:1≤x≤14,
故答案为: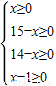 ,1≤x≤14,
,1≤x≤14,
列表为:
描点并连线为:
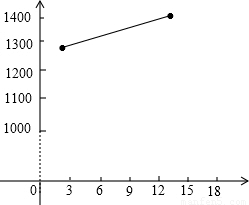
(4)∵y=10x+1270,
∴k=10>0,
∴y随x的增大而增大,
∵1≤x≤14,
∴当x=1时,y最小=1280(万吨),
∴调运方案为:
从A到家调运1万吨,从A到乙调运13万吨,从B到甲调运14万吨,从B到乙调运0万吨.
点评:本题考查了代数式的运用,函数解析式的求法,列表法画函数图象的运用及运用一次函数的解析式的性质进行方案设计的运用.
(2)根据影响水的调运量的两个因素通过(1)的代数式就可以求出调运总量为y万吨•千米与x之间的函数关系式;
(3)根据题意中的隐含条件和问题的实际意义建立不等式组求出其解就可以确定自变量的取值范围,再利用描点法就可以画出函数图象;
(4)由(2)的解析式和(3)的自变量的取值范围就可以最小调运量的方案.
解答:解:(1)设从A水库调往甲地的水量为x万吨,由题意得:
从A水库调往乙地的水量为:(14-x)吨,
从B水库调往甲地的水量为:(15-x)吨,
从B水库调往乙地的水量为:(x-1)吨,
故答案为:14-x,15-x,x-1;
(2)设水的调运总量为y万吨•千米,由题意,得
y=50x+30(14-x)+60(15-x)+50(x-1),
=10x+1270,
故答案为:10x+1270;
(3)由题意得:
 ,
,解得:1≤x≤14,
故答案为:
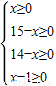 ,1≤x≤14,
,1≤x≤14,列表为:
| x | 1 | 14 |
| y=10x+1270 | 1280 | 1410 |

(4)∵y=10x+1270,
∴k=10>0,
∴y随x的增大而增大,
∵1≤x≤14,
∴当x=1时,y最小=1280(万吨),
∴调运方案为:
从A到家调运1万吨,从A到乙调运13万吨,从B到甲调运14万吨,从B到乙调运0万吨.
点评:本题考查了代数式的运用,函数解析式的求法,列表法画函数图象的运用及运用一次函数的解析式的性质进行方案设计的运用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
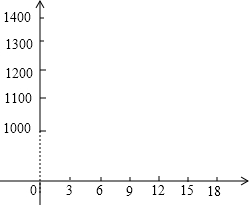 万吨•千米)尽可能小.
万吨•千米)尽可能小.