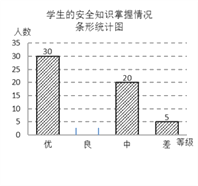
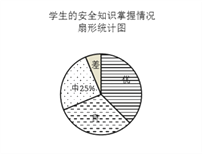
题目内容
【题目】已知抛物线![]() ,
,
![]() 求抛物线与
求抛物线与![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与
求抛物线与![]() 轴的两个交点及两个交点间的距离.
轴的两个交点及两个交点间的距离.
![]() 求抛物线与
求抛物线与![]() 轴的交点及与
轴的交点及与![]() 轴交点所围成的三角形面积.
轴交点所围成的三角形面积.
![]() 把抛物线
把抛物线![]() 改为顶点式,说明顶点和对称轴.
改为顶点式,说明顶点和对称轴.
【答案】![]() 抛物线与
抛物线与![]() 轴的交点坐标为
轴的交点坐标为![]() ;
;![]() 两个交点间的距离
两个交点间的距离![]() ;(3)12;
;(3)12;![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() ,对称轴为直线
,对称轴为直线![]() .
.
【解析】
(1)根据y轴上点的坐标特征,求出自变量为0时的函数值即可;
(2)根据抛物线与x轴的交点问题,解方程-2x2-4x+6=0即可得到抛物线与x轴的交点坐标,然后利用两个交点的横坐标之差得到两交点的距离;
(3)根据三角形面积公式计算;
(4)先利用配方法把一般式化为顶点式y=-2(x+1)2+8,然后根据二次函数的性质求解.
![]() 把
把![]() 代入
代入![]() 得
得![]() ,
,
所以抛物线与![]() 轴的交点坐标为
轴的交点坐标为![]() ;
;
![]() 把
把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,![]() ,
,
所以抛物线与![]() 轴的两个交点坐标为
轴的两个交点坐标为![]() 、
、![]() ,两个交点间的距离
,两个交点间的距离![]() ;
;
![]() 抛物线与
抛物线与![]() 轴的交点及与
轴的交点及与![]() 轴交点所围成的三角形面积
轴交点所围成的三角形面积![]() ;(4)
;(4)![]() ,
,
所以抛物线的顶点坐标为![]() ,对称轴为直线
,对称轴为直线![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.