题目内容
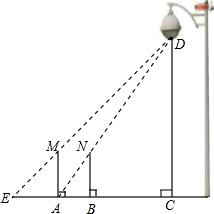（2013•陕西）一天晚上，黎明和张龙利用灯光下的影子长来测量一路灯D的高度．如图，当李明走到点A处时，张龙测得李明直立时身高AM与影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m，已知李明直立时的身高为1.75m，求路灯的高CD的长．（结果精确到0.1m）．分析：根据AM⊥EC，CD⊥EC，BN⊥EC，EA=MA得到MA∥CD∥BN，从而得到△ABN∽△ACD，利用相似三角形对应边的比相等列出比例式求解即可．
解答：解：设CD长为x米，
∵AM⊥EC，CD⊥EC，BN⊥EC，EA=MA
∴MA∥CD∥BN
∴EC=CD=x
∴△ABN∽△ACD，
∴
=
即
=
解得：x=6.125≈6.1．
∴路灯高CD约为6.1米．
∵AM⊥EC，CD⊥EC，BN⊥EC，EA=MA
∴MA∥CD∥BN
∴EC=CD=x
∴△ABN∽△ACD，
∴
| BN |
| CD |
| AB |
| AC |
即
| 1.75 |
| x |
| 1.25 |
| x-1.75 |
解得：x=6.125≈6.1．
∴路灯高CD约为6.1米．
点评：本题考查了相似三角形的应用，解题的关键是根据已知条件得到平行线，从而证得相似三角形．
练习册系列答案
相关题目
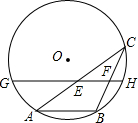（2013•陕西）如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为
