题目内容
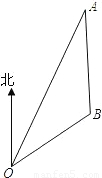
如图,在海岸边有一港口O,已知小岛A在港口O北偏东30°的方向上,小岛B在小岛A的正南方向,OA=60海里,OB=20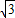 海里.
海里.(1)求O到直线AB的距离;
(2)小岛B在港口O的什么方向上?
【答案】分析:本题可通过辅助线构造直角三角形来求解,OC为直角三角形AOC和BOC的公共直角边,可先再直角三角形AOC中求出OC的长,然后在直角三角形BOC中求出∠OBC的度数.
解答: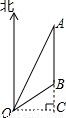 解:(1)过O作OC⊥AB交AB的延长线于C,那么OC就是所求的距离,
解:(1)过O作OC⊥AB交AB的延长线于C,那么OC就是所求的距离,
Rt△AOC中,∠A=30°,OA=60,
OC=AC•sin30°=30海里,
即:O到AB的距离是30海里;
(2)在Rt△OBC中,
∵OB=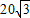 ,OC=30,
,OC=30,
∴sin∠OBC=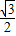 .
.
∴∠OBC=60°.
∴B在港口O的北偏东60°方向上.
点评:本题可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题解决.
解答:
 解:(1)过O作OC⊥AB交AB的延长线于C,那么OC就是所求的距离,
解:(1)过O作OC⊥AB交AB的延长线于C,那么OC就是所求的距离,Rt△AOC中,∠A=30°,OA=60,
OC=AC•sin30°=30海里,
即:O到AB的距离是30海里;
(2)在Rt△OBC中,
∵OB=
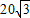 ,OC=30,
,OC=30,∴sin∠OBC=
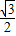 .
.∴∠OBC=60°.
∴B在港口O的北偏东60°方向上.
点评:本题可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题解决.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
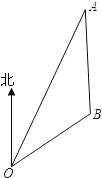 如图,在海岸边有一港口O.已知:小岛A在港口O北偏东30°的方向,小岛B在小岛A正南方向,OA=60海里,OB=20
如图,在海岸边有一港口O.已知:小岛A在港口O北偏东30°的方向,小岛B在小岛A正南方向,OA=60海里,OB=20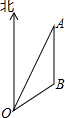 如图,在海岸边有一港口O,已知小岛A在港口O北偏东30°的方向上,小岛B在小岛A的正南方向,OA=60海里,OB=20
如图,在海岸边有一港口O,已知小岛A在港口O北偏东30°的方向上,小岛B在小岛A的正南方向,OA=60海里,OB=20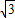 海里.计算:
海里.计算: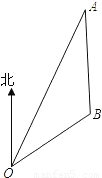
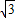 海里.计算:
海里.计算: