��Ŀ����
�����������ɴ�1��ʼ��������Ȼ����ɣ��۲���ɲ���ɸ���Ľ��
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
��������������������
��1�����е�8�е����һ������______________��������Ȼ��_____________��ƽ������8�й���____________������
��2���ú�n�Ĵ���ʽ��ʾ����n�еĵ�һ������___________________�����һ������
________________����n���_______________������
��3�����n�и���֮�ͣ�
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
��������������������
��1�����е�8�е����һ������______________��������Ȼ��_____________��ƽ������8�й���____________������
��2���ú�n�Ĵ���ʽ��ʾ����n�еĵ�һ������___________________�����һ������
________________����n���_______________������
��3�����n�и���֮�ͣ�
�Խ⣺(1)64��8��15��
��2��n2-2n+2��n2��(2n-1);
��3����n�и���֮�ͣ�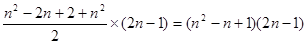
��2��n2-2n+2��n2��(2n-1);
��3����n�и���֮�ͣ�
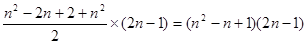
��1���۲�������֪�����е�8�е����һ������64��������Ȼ��8��ƽ������8�й���15�������ʴ�Ϊ��64��8��15��
��2���ɣ�1���ó�һ����ɣ���n�еĵ�һ�����ǣ�n-1��2+1�����һ������n2����n�й�2n-1������
�ʴ�Ϊ����n-1��2+1��n2��2n-1��
��3����n�е�һ����Ϊ��n-1��2+1�����һ��Ϊn2 �ܹ�2n-1����
���Ե�n�и���֮��=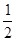 [��n-1��2+1+n2]����2n-1��=��n2-n+1����2n-1��
[��n-1��2+1+n2]����2n-1��=��n2-n+1����2n-1��
��2���ɣ�1���ó�һ����ɣ���n�еĵ�һ�����ǣ�n-1��2+1�����һ������n2����n�й�2n-1������
�ʴ�Ϊ����n-1��2+1��n2��2n-1��
��3����n�е�һ����Ϊ��n-1��2+1�����һ��Ϊn2 �ܹ�2n-1����
���Ե�n�и���֮��=
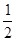 [��n-1��2+1+n2]����2n-1��=��n2-n+1����2n-1��
[��n-1��2+1+n2]����2n-1��=��n2-n+1����2n-1��
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
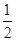 ���෴���ǣ�����
���෴���ǣ�����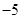 �棬����4�����¶�Ϊ
�棬����4�����¶�Ϊ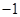 ��
��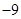 ��
��
 ��
��