题目内容
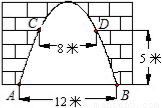
如图,某地一城墙门洞呈抛物线形,已知门洞的地面宽度AB=12米,两侧距地面5米高C、D处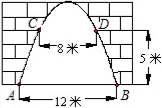 各安装一盏路灯,两灯间的水平距离CD=8米,
各安装一盏路灯,两灯间的水平距离CD=8米,(1)求这个门洞的高度
(2)现有体宽均约为0.5水,身高约为1.6米的20名同学想要手挽手成一排横向通过该城门,请你测算,他们能否通过?
分析:(1)设出抛物线的函数关系式,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,即可得出A、B、C、D点的坐标,代入函数式求解即可.
(2)由题意可以得出组成的长为0.5×20,高为1.6的矩形人墙,令x=5代入代入函数式,得出y值,比较y与1.6的大小,即可得出结论.
(2)由题意可以得出组成的长为0.5×20,高为1.6的矩形人墙,令x=5代入代入函数式,得出y值,比较y与1.6的大小,即可得出结论.
解答:解:(1)如图建立坐标系:
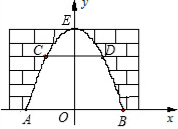
则可得:A点坐标为(-6,0),B点为(6,0),C点为(-4,5),D点为(4,5),
设抛物线的函数式为y=ax2+bx+c,把点的坐标代入函数式得:
,
解得:
,
∴函数式为y=-
x2+9,
即E点坐标为(9,0),
∴门洞的高为9米.
(2)能.
由题意得x=
×0.5×20=5,
把x=5代入函数式得y=-
×25+9=2.75>1.6,
∴可以通过.

则可得:A点坐标为(-6,0),B点为(6,0),C点为(-4,5),D点为(4,5),
设抛物线的函数式为y=ax2+bx+c,把点的坐标代入函数式得:
|
解得:
|
∴函数式为y=-
| 1 |
| 4 |
即E点坐标为(9,0),
∴门洞的高为9米.
(2)能.
由题意得x=
| 1 |
| 2 |
把x=5代入函数式得y=-
| 1 |
| 4 |
∴可以通过.
点评:本题考查了二次函数的性质.求解二次函数一般的方法是:先设出函数表达式,根据点的坐标利用待定系数法求解.

练习册系列答案
相关题目


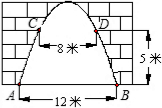 各安装一盏路灯,两灯间的水平距离CD=8米,
各安装一盏路灯,两灯间的水平距离CD=8米,