题目内容
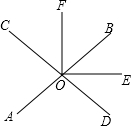 如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°(
∴∠
∵OE平分∠BOD( 已知 )
∴∠BOE=
| 1 |
| 2 |
∵OF⊥OE( 已知 )
∴∠EOF=
∵∠BOF+∠BOE=∠EOF
∴∠BOF=
考点:垂线,对顶角、邻补角
专题:推理填空题
分析:利用对顶角的性质以及角平分线的性质得出∠BOE的度数,再利用垂直定义得出∠BOF的度数.
解答:解:∵∠BOD=∠AOC(对顶角相等),∠AOC=60°( 已知)
∴∠BOD=60°
∵OE平分∠BOD( 已知 )
∴∠BOE=
∠BOD=30°( 角平分线的性质)
∵OF⊥OE( 已知 )
∴∠EOF=90°( 垂直定义 )
∵∠BOF+∠BOE=∠EOF
∴∠BOF=60°.
∴∠BOD=60°
∵OE平分∠BOD( 已知 )
∴∠BOE=
| 1 |
| 2 |
∵OF⊥OE( 已知 )
∴∠EOF=90°( 垂直定义 )
∵∠BOF+∠BOE=∠EOF
∴∠BOF=60°.
点评:此题主要考查了垂直定义以及对顶角和角平分线的性质,得出∠BOE的度数是解题关键.

练习册系列答案
相关题目
下列角度中,不能成为多边形内角和的是( )
| A、540° | B、800° |
| C、900° | D、1800° |
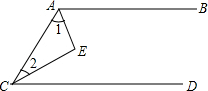 如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD,求证:∠1+∠2=90°.
如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD,求证:∠1+∠2=90°.