题目内容
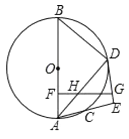
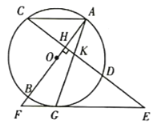
【题目】如图,已知![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过
,过![]() 的延长线上一点
的延长线上一点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,切点为点
,切点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE,即可得到结果;
(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;
(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.
解:(1)证明:如图1,连接![]() ,
,
![]() 为
为![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴△EKG是等腰三角形;
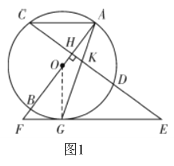
(2)证明:如图2,连接![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
![]()
(3)解:如图3,连接![]() ,
,![]() ,
,
由![]() ,可设
,可设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
![]() ,
,![]() ,
,
设![]() 的半径为
的半径为![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() 为
为![]() 的切线,
的切线,
![]() 为直角三角形,
为直角三角形,
在![]() 中,
中,![]() ,
,
![]() ,
,
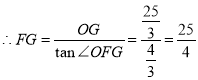 .
.

练习册系列答案
相关题目
【题目】某工厂对一批灯泡的质量进行随机抽查,见下表:
抽取灯泡数 | 40 | 100 | 150 | 500 | 1000 | 1500 |
优等品数 | 36 | 92 | 145 | 474 | 950 | 1427 |
优等品频率 |
(1)计算表中的优等品的频率(精确到0.001)
(2)根据抽査的灯泡优等品的频率,估计这批灯泡优等品的概率(精确到0.01)