Question

根据要求拟编一道新题．
已知：如图所示，在矩形ABCD所在平面有一点P，且PA=PD，请说明：PB=PC．
请你将上述条件中的“矩形ABCD”改为另一种四边形，其余条件不变，使结论“PB=PC”仍然成立，再根据改编后的题目画出图形，并说明理由．

Answer 1

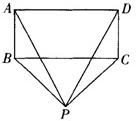
解：在等腰梯形ABCD所在平面有一点P，且PA=PD，请说明：PB=PC．
如图：
∵PA=PD，
∴点P一定在AD的垂直平分线上，
又∵AD与BC的中垂线是同一条直线，
∴点P一定在BC的垂直平分线上，
∴PB=PC．
分析：根据矩形一边的中垂线也是对边的中垂线的这个性质，可将矩形改为等腰梯形．
点评：考查了矩形和等腰梯形都是轴对称图形，还考查了线段垂直平分线的性质：线段垂直平分线上的点到线段两个端点的距离相等．