题目内容

【多彩数学】
如何将正方形的边三等分和五等分
给你一张如图1的正方形纸片，让你用折纸的方法将其中一边二、四等分，你会轻而易举地用对折的方法完成．可是让你将正方形的一边三等分或五等分呢？我们先来三等分边长．

（1）对折，使E为BC中点（图2）；
（2）连结DE，沿DE将DC翻折到DF位置（图3）；
（3）使点A与点F重合（图4），那么AG=
13
AB，G为AB的三等分点．
下面请你试一试将正方形一边长五等分的折叠方法写出来．
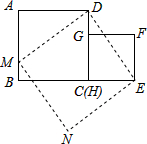
分析：先根据把正方形的一边三等分的方法对到E点，BE=
1
3
BC，沿DE将DC翻折到DF位置；使点A与点F重合，设AB=5a，则CE=
10
3
a，RF=
10
3
a，BE=
5a
3
，AG=t，则GF=t，GB=5a-t，然后利用勾股定理可计算出t=a．
解答：解：①先把正方形的一边三等分，即点E为BC的三等分点，BE=
1
3
BC，；
②连结DE，沿DE将DC翻折到DF位置；
③使点A与点F重合，那么AG=
1
5
AB，G为AB的五等分点．如图．
点评：本题考查了折叠的性质：翻折变换（折叠问题）实质上就是轴对称变换；折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
（2012•李沧区一模）【问题引入】
几个人拎着水桶在一个水龙头前面排队打水，水桶有大有小．他们该怎样排队才能使得总的排队时间最短？
假设只有两个人时，设大桶接满水需要T分钟，小桶接满水需要t分钟（显然T＞t），若拎着大桶者在拎着小桶者之前，则拎大桶者可直接接水，只需等候T分钟，拎小桶者一共等候了（T+t）分钟，两人一共等候了（2T+t）分钟；反之，若拎小桶者在拎大桶者前面，容易求出出两人接满水等候（T+2t）分钟．可见，要使总的排队时间最短，拎小桶者应排在拎大桶者前面．这样，我们可以猜测，几个人拎着水桶在一个水龙头前面排队打水，要使总的排队时间最短，需将他们按水桶从小到大排队．
规律总结：
事实上，只要不按从小到大的顺序排队，就至少有紧挨着的两个人拎着大桶者排在拎小桶者之前，仍设大桶接满水需要T分钟，小桶接满水需要t分钟，并设拎大桶者开始接水时已等候了m分钟，这样拎大桶者接满水一共等候了（m+T）分钟，拎小桶者一共等候了（m+T+t）分钟，两人一共等候了（2m+2T+t）分钟，在其他人位置不变的前提下，让这两个人交还位置，即局部调整这两个人的位置，同样介意计算两个人接满水共等候了
2m+2t+T
2m+2t+T
分钟，共节省了
T-t
T-t
分钟，而其他人等候的时间未变，这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者之前都可以这样调整，从而使得总等候时间减少．这样经过一系列调整后，整个队伍都是从小打到排列，就打到最优状态，总的排队时间就最短．
【方法探究】
一般的，对某些设计多个可变对象的数学问题，先对其少数对象进行调整，其他对象暂时保持不变，从而化难为易，取得问题的局部解决．经过若干次这种局部的调整，不断缩小范围，逐步逼近目标，最终使问题得到解决，这种数学思想就叫做局部调整法．
【实践应用1】
如图1在锐角△ABC中，AB=4
2
，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？
解析：
（1）先假定N为定点，调整M到合适的位置使BM+MN有最小值（相对的），容易想到，在AC上作AN′=AN（即作点N关于AD的对称点N'），连接BN′交AD于M，则M点是使BM+MN有相对最小值的点．（如图2，M点是确定方法找到的）
（2）在考虑点N的位置，使BM+MN最终达到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使
BM+MN′=BN′
BM+MN′=BN′
，此时BM+MN的最小值是
4
4
．
【实践应用2】
如图3，把边长是3的正方形等分成9个小正方形，在有阴影的小正方形内（包括边界）分别取点P、R，于已知格点Q（每个小正方形的顶点叫做格点）构成三角形，则△PQR的最大面积是
2
2
，请在图4中画出面积最大时的△PQR的图形．
【问题提出】如何把n个正方形拼接成一个大正方形？
为解决上面问题，我们先从最基本，最特殊的情形入手．对于边长为a的两个正方形ABCD和EFGH，如何把它们拼接成一个正方形？
【问题解决】对于边长为a的两个正方形ABCD和EFGH，按图所示的方式摆放，在沿虚线BD，EG剪开后，可以按图中所示的移动方式拼接为图中的四边形BNED．从拼接的过程容易得到结论：
①四边形BNED是正方形；
②S正方形ABCD+S正方形EFGH=S正方形BNED．
【类比应用】
对于边长分别为a，b（a＞b）的两个正方形ABCD和EFGH，按图所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．明四边形MNED是正方形，并请你用含a，b的代数式表示正方形MNED的面积；
②如图，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简略说明你的拼接方法（类比如图，用数字表示对应的图形直接画在图中）．
【拓广延伸】对于n（n是大于2的自然数）个任意的正方形，能否通过若干次拼接，将其拼接成为一个正方形？请简要说明你的理由．

．（6分）如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax2＋ax－2上，点C的坐标为(－1，0)．

1.(1)点A的坐标为         ，点B的坐标为        ；

2.(2)抛物线的关系式为                      ，其顶点坐标为            ；

【小题】(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．请判断点、是否在(2)中的抛物线上，并说明理由．

 

．（6分）如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax2＋ax－2上，点C的坐标为(－1，0)．

1.(1)点A的坐标为         ，点B的坐标为         ；

2.(2)抛物线的关系式为                       ，其顶点坐标为             ；

【小题】(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．请判断点、是否在(2)中的抛物线上，并说明理由．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网