题目内容
课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.为此,他们对水槽的横截面进行了如下探索:
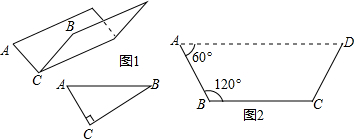
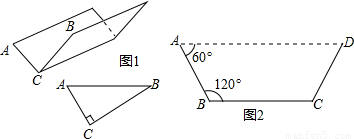
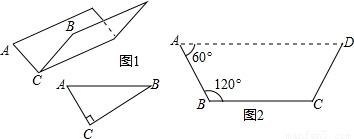
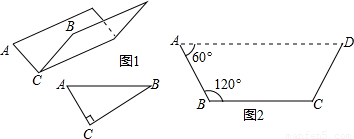
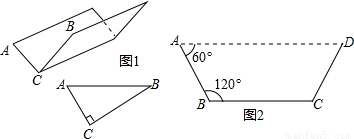
(1)方案①:把它折成横截面为直角三角形的水槽(如图1).
若∠ACB=90°,设AC=x厘米,该水槽的横截面面积为y厘米2,请你写出y关于x的函数关系式(不必写出x的取值范围),并求出当x取何值时,y的值最大,最大值又是多少?
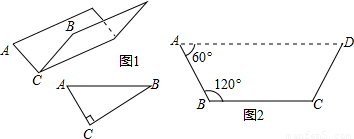
方案②:把它折成横截面为等腰梯形的水槽(如图2).
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小;
(2)假如你是该兴趣小组中的成员,请你再提供两种方案,使你所设计的水槽的横截面面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).
【答案】分析:(1)①已知正方形的周长,可求出其边长,即AC+BC的长,即可表示出BC的长,然后根据直角三角形的面积公式即可得出y,x的函数关系式,根据函数的性质即可求出y的最大值.
②本题已知了AB+BC+CD=正方形的边长,可设AB为x,那么CD也为x,BC可用正方形的边长求得.过B、C作AD的垂线,通过构建的直角三角形,用x表示出BE和AE的长,即可求出上底AD的长,然后根据梯形的面积公式即可求得y,x的函数关系式,根据函数的性质即可求得函数的最大值;
(2)由(1)的结果大致可推断出折的边数越多,面积越大,因此折的边数无限多即折的图形为半圆时面积最大,据此可列出不同的方案.
解答: 解:
解:
(1)①y=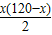 ,
,
当x=60时,y最大值=1800;
②过点B作BE⊥AD于E,CF⊥AD于F,
设AB=CD=xcm,梯形的面积为Scm2,则BC=EF=(120-2x)cm,
AE=DF= x,BE=CF=
x,BE=CF=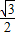 x,AD=120-x,
x,AD=120-x,
∴S= •
•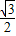 x(240-3x)
x(240-3x)
当x=40,S最大值=1200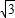 ,
,
S最大值>y最大值;
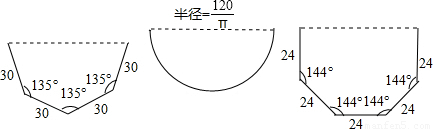
(2)方案:①正八边形一半,②正十边形一半,③半圆等.
点评:本题主要考查了图形面积的求法和二次函数的应用.
②本题已知了AB+BC+CD=正方形的边长,可设AB为x,那么CD也为x,BC可用正方形的边长求得.过B、C作AD的垂线,通过构建的直角三角形,用x表示出BE和AE的长,即可求出上底AD的长,然后根据梯形的面积公式即可求得y,x的函数关系式,根据函数的性质即可求得函数的最大值;
(2)由(1)的结果大致可推断出折的边数越多,面积越大,因此折的边数无限多即折的图形为半圆时面积最大,据此可列出不同的方案.
解答:
 解:
解:(1)①y=
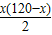 ,
,当x=60时,y最大值=1800;
②过点B作BE⊥AD于E,CF⊥AD于F,
设AB=CD=xcm,梯形的面积为Scm2,则BC=EF=(120-2x)cm,
AE=DF=
 x,BE=CF=
x,BE=CF=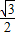 x,AD=120-x,
x,AD=120-x,∴S=
 •
•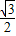 x(240-3x)
x(240-3x)当x=40,S最大值=1200
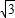 ,
,S最大值>y最大值;

(2)方案:①正八边形一半,②正十边形一半,③半圆等.
点评:本题主要考查了图形面积的求法和二次函数的应用.

练习册系列答案
相关题目