题目内容
某新建的大楼楼体外表需贴磁砖,楼体外表总面积为4800m2.(1)设所需磁砖的块数为n(块),每块磁砖的面积为S(m2),试求n与S的函数关系式;
(2)如果每块磁砖的面积均为80cm2,每箱磁砖有120块,需买磁砖多少箱?
分析:(1)可以由:所需磁砖的块数=楼体外表总面积÷每块磁砖的面积,这个关系式列出n与S的函数关系
式;
(2)因第一问已列出n与s的函数关系式,将s=80代入它可得所需磁砖的块数,再由:需买磁砖的箱数=
所需磁砖的块数÷每箱磁砖的块数,这个关系式求出需买磁砖的箱数即可.
式;
(2)因第一问已列出n与s的函数关系式,将s=80代入它可得所需磁砖的块数,再由:需买磁砖的箱数=
所需磁砖的块数÷每箱磁砖的块数,这个关系式求出需买磁砖的箱数即可.
解答:解:(1)所需磁砖的块数=楼体外表总面积÷每块磁砖的面积
所以由此可得出,
n与S的函数关系式是:n=
;
(2)当s=80时,n=
=6×105,
需买磁砖的箱数=所需磁砖的块数÷每箱磁砖的块数
所以由此可得出,
需买磁砖的箱数是
=5000(箱)
答:需买磁砖的箱数5000箱.
所以由此可得出,
n与S的函数关系式是:n=
| 4800 |
| s |
(2)当s=80时,n=
| 4800 |
| 80×10-4 |
需买磁砖的箱数=所需磁砖的块数÷每箱磁砖的块数
所以由此可得出,
需买磁砖的箱数是
| 6×105 |
| 120 |
答:需买磁砖的箱数5000箱.
点评:本题主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,根据自变量的值求算对应的函数值.

练习册系列答案
相关题目
 。
。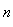 (块),每块磁砖的面积为
(块),每块磁砖的面积为 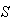 (
( ),试求
),试求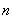 与
与  的函数关系式;
的函数关系式;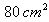 ,每箱磁砖有120块,需买磁砖多少箱?
,每箱磁砖有120块,需买磁砖多少箱?