��Ŀ����
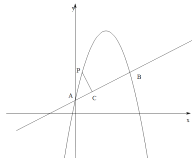
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬����A��y���ϣ���B�ĺ�����Ϊ4��PΪ��������һ���㣬����P��PC��ֱ��AB������ΪC.
����A��B���㣬����A��y���ϣ���B�ĺ�����Ϊ4��PΪ��������һ���㣬����P��PC��ֱ��AB������ΪC.
��1���������ߵĽ���ʽ��
��2������P��ֱ��AB�Ϸ����������ϣ���P�ĺ�����Ϊm����m�Ĵ���ʽ��ʾ�߶�PC�ij���������߶�PC�����ֵ����ʱ��P������.
��3������P��������������һ�㣬������0�㣼��PAB��45�㡣��ֱ��д����
�ٵ�P�ĺ������ȡֵ��Χ��
��������Ϊ������PΪ���ɵ㡱�����ɵ㡱�ĸ�����

���𰸡���1��![]()
��2��![]() ��
�� ![]()
��3��![]() ��
��![]() 7��.
7��.
�������������������1�����A��B����������������ߵĽ���ʽ���ɽ�����⣮
��2����PF��x����F����AB��E��ֱ��AB��x����D����P��m��-m2+![]() m+1������E��m��
m+1������E��m�� ![]() m+1����PE=-m2+4m���ɡ�PCE�ס�DOA���ɵ�
m+1����PE=-m2+4m���ɡ�PCE�ס�DOA���ɵ�![]() ���������κ����ɽ�����⣮
���������κ����ɽ�����⣮
��3������ͼ2�У�ȡ��F��1��4��������AF��FB������֤����FAB�ǵ���ֱ�������Σ��Ƴ���FAB=45�㣬��ֱ��AF����������P���ɵ�ֱ��AF�Ľ���ʽΪy=3x+1�����÷����������PAB=45��ʱ����P�����꼴�ɽ�����⣬�ٸ��ݶԳ������P��A��PAʱ�ĵ�P������꼴�ɽ�����⣮
�ڹ۲�ͼ���֪��P��������ķ�Χ3��yp��![]() ��-
��-![]() ��yP��3����������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����
��yP��3����������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����![]() ��m��4���Ƴ���Ӧ�ĵ�P��7����
��m��4���Ƴ���Ӧ�ĵ�P��7����
�����������1��������A��0��1����B��4��3����
��A��0��1����B��4��3������y=-x2+bx+c�õ�
![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪy=-x2+![]() x+1��
x+1��
��2����PF��x����F����AB��E��ֱ��AB��x����D��
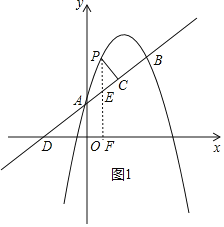
������D��-2��0����A��0��1����
��P��m��-m2+![]() m+1������E��m��
m+1������E��m�� ![]() m+1����PE=-m2+4m
m+1����PE=-m2+4m
��OA=1��OD=2��AD=![]() ��
��
��PF��OA��
���DAO=��DEF=��PEC��
�ߡ�AOD=��PCE=90�㣬
���PCE�ס�DOA��
��![]() ��
��
��![]() ��
��
��PC=-![]() ��m2-4m����
��m2-4m����
��PC=-![]() ��m2-4m��=-
��m2-4m��=-![]() ��m-2��2+
��m-2��2+![]() ��
��
��-![]() ��0��
��0��
��m=2ʱ��PC�����ֵ�����ֵΪ![]() ����ʱP��2��6����
����ʱP��2��6����
��3������ͼ2�У�ȡ��F��1��4��������AF��FB��

��A��0��1����B��4��3����
��AF=![]() ��FB=
��FB=![]() ��AB=
��AB=![]()
��AF=FB��AF2+BF2=AB2��
���FAB�ǵ���ֱ�������Σ�
���FAB=45������ֱ��AF����������P��
��ֱ��AF�Ľ���ʽΪy=3x+1��
��
���![]() ��
��![]() ��
��
��A��0��1����
��P��![]() ��
�� ![]() ����
����
��P��A��PAʱ��
ֱ��P��A�Ľ���ʽΪy=-![]() x+1��
x+1��
�� �����
�����![]() ��
�� ��
��
��P����![]() ��-
��-![]() ��
��
��۲�ͼ���֪����������0�㣼��PAB��45��ĵ�P�ĺ�����![]() ��m��4��4��m��
��m��4��4��m��![]() ��
��
�ڹ۲�ͼ���֪��P��������ķ�Χ3��yp��![]() ��-
��-![]() ��yP��3
��yP��3
������ypΪ4��5��6��0��1��2���ֵ�P�ĺ�����![]() ��m��4��4��m��
��m��4��4��m��![]() ��
��
���Ӧ�ĵ�P��7����
�ࡰ�ɵ㡱�ĸ���Ϊ7����