Question

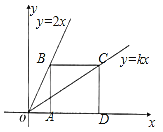
【题目】如图，点B、C分别在直线y=2x和y=kx上，点A、D是x轴上的两点，且四边形ABCD是正方形．

（1）若正方形ABCD的边长为2，则点B、C的坐标分别为　 　．

（2）若正方形ABCD的边长为a，求k的值．

Answer 1

【答案】（1）（1，2），（3，2）（2）

【解析】

（1）根据正方形的边长，运用正方形的性质表示出点B、C的坐标；

（2）根据正方形的边长，运用正方形的性质表示出C点的坐标，再将C的坐标代入函数中，从而可求得k的值．

（1）∵正方形边长为2，

∴AB=2，

在直线y=2x中，当y=2时，x=1，

∴B（1，2），

∵OA=1，OD=1+2=3，

∴C（3，2），

故答案为：（1，2），（3，2）；

（2）∵正方形边长为a，

∴AB=a，

在直线y=2x中，当y=a时，x=，

∴OA=，OD=，

∴C（，a），

将C（，a）代入y=kx，得a=k×，

解得：k=，

故答案为：.