Question

（1）如图甲所示，可得阴影部分的面积是________（写成多项式的形式）；
（2）如图乙所示，若将阴影部分裁剪下来重新拼成一个长方形，它的长是________，宽是________，面积是________（写成两式乘积形式）；
（3）比较图甲和图乙中阴影部分的面积，可得乘法公式________；
（4）利用公式计算（-2x+y）（2x+y）=________．

Answer 1

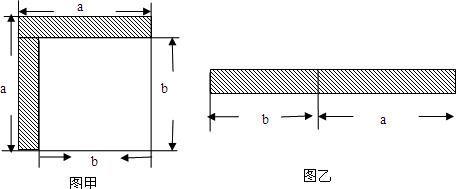
解：（1）利用正方形的面积公式可知：阴影部分的面积=a²-b²；

（2）a+b，a-b，（a+b）（a-b）；

（3）（a+b）（a-b）=a²-b²（等式两边交换位置也可）；

（4）①原式=（10+0.2）×（10-0.2），
=10²-0.2²，
=100-0.04，
=99.96；
②原式=（y+2x）（y-2x）
=（y）²-（2x）²，
=y²-4x²．

故答案是：（1）a²-b²
（2）a-b，a+b，（a+b）（a-b）；
（3）（a+b）（a-b）=a²-b²
（4）y²-4x²．
分析：（1）利用正方形的面积公式就可求出；
（2）仔细观察图形就会知道长，宽由面积公式就可求出面积；
（3）建立等式就可得出；
（4）利用平方差公式就可方便简单的计算．
点评：此题主要考查了平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．对于有图形的题同学们注意利用数形结合求解更形象直观．